Rotazioni dei corpi rigidi - parte 5

---

In questa puntata voglio spiegare, possibilmente in termini semplici, una serie di concetti:

1. Come si rappresentano i corpi rigidi nello spazio tridimensionale, perché nella robotica tradizionale si fa l’ipotesi che le varie parti di un robot siano perfettamente rigide. Questo significa che durante il moto non subiscono deformazioni pur essendo sottoposte a forze interne o esterne di valore arbitrario, anche grande. E’ un’ipotesi un po’ inverosimile, ma ci fa molto comodo e in pratica i costruttori di robot cercano di aumentare la rigidezza delle strutture per evitare fenomeni di vibrazione che impediscono movimenti accurati. Se non si capiscono i moti rigidi, risulta poi difficile capire i moti non rigidi, che sono quelli più comuni.

2. Come si rappresentano i moti dei corpi rigidi. I moti dei corpi rigidi sono solo due: il primo consiste in quella che si definisce una traslazione: il corpo si muove lungo una direzione, ma non cambia il suo orientamento (che viene chiamato anche “assetto”). Il secondo in quella che si definisce una rotazione: il corpo varia il suo assetto, ruotando intorno ad un asse nello spazio. I due moti si possono comporre per ottenere le cosiddette roto-traslazioni, che poi sono i moti più comuni che possiamo osservare. Pensate ad esempio ad un pattinatore che scivola e piroetta sul ghiaccio: pur non essendo un corpo rigido, possiamo apprezzare come si sposti e contemporaneamente ruoti: questa è appunto una serie di roto-traslazioni nel tempo.

3. Come si rappresentano matematicamente le roto-traslazioni, cioè quali sono le strutture matematiche che ci permettono di descrivere i moti dei corpi rigidi, di comporli tra loro, di ricavare i parametri cinematici coinvolti e molte altre cosette interessanti.

Una volta chiariti questi tre punti, siamo praticamente pronti per partire nel viaggio di scoperta della cinematica dei robot.

In questo post è possibile che ripeta cose già dette in precedenza, ma dovete avere pazienza, magari è utile e sicuramente non è dannoso.

Corpi rigidi

Prendiamo un oggetto qualunque posto nello spazio tridimensionale, facciamo l’ipotesi che sia rigido e pensiamo a come poter descrivere il suo stato.

Ci possono essere molti modi per descrivere lo stato di un corpo, ad esempio il specificandone il colore, o la forma, o le proprietà della sostanza di cui è composto, ecc. Ma noi siamo interessati al suo moto, che è un concetto relativo, cioè il moto è la variazione di posizione (e assetto) di qualcosa rispetto a qualcos’altro.

In questo senso, il modo più semplice per individuarne lo stato è quello di di associare all’oggetto un sistema di riferimento cartesiano destrorso, cioè una terna di vettori a lunghezza unitaria, tra loro mutuamente ortogonali, che “partono” tutti da un punto comune $O$ detto origine.

I tre vettori (l’avevamo già visto in precedenza) li indichiamo con $\ivet,\jvet$ e $\kvet$. Essi hanno norma unitaria, cioè

$||\ivet||=||\jvet||=||\kvet||=1$ e devono obbedire a queste relazioni, che contraddistinguono i sistemi cartesiani destrorsi

$$\ivet\times\jvet=\kvet\quad\quad \jvet\times\kvet=\ivet\quad\quad \kvet\times\ivet=\jvet$$

dove il simbolo $\times$ sta ad indicare il prodotto vettoriale o prodotto esterno. Non vi spiego che cos’è e come si calcola il prodotto vettoriale, perché dovreste saperlo e se non lo sapete, nel Web ci sono moltisimi siti che lo spiegano.

In ogni caso un sistema di riferimento destrorso ha l’aspetto che vedete nella Figura sottostante

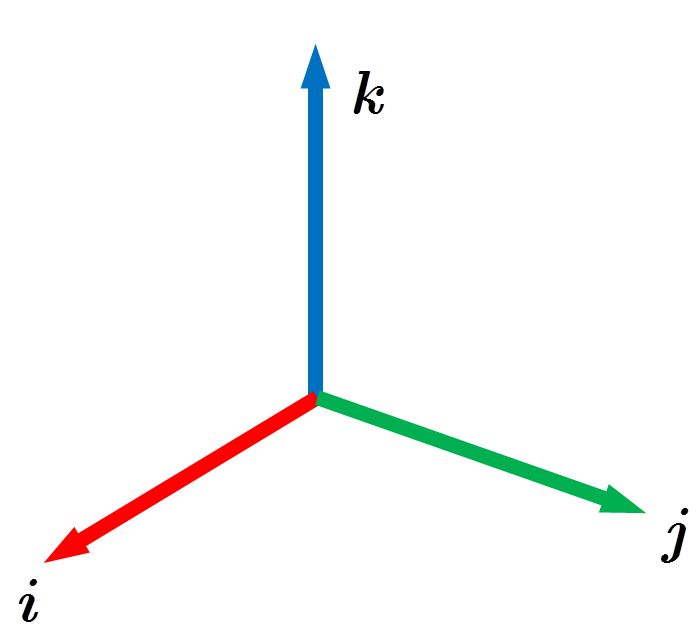
Il vettore unitario $\ivet$ individua la direzione $x$ e di solito lo si colora di rosso, il vettore unitario $\jvet$ individua la direzione $y$ e di solito lo si colora di verde, il vettore unitario $\kvet$ individua la direzione $z$ e di solito lo si colora di blu. Il significato dei colori è intuitivo: ogni colore è costituito da una mistura delle tre componenti primarie rosso-verde-blu (in inglese red-gren-blue o più semplicemente RGB), così come ogni punto geometrico dello spazio è costituito da una “mistura” delle tre componenti rispetto ai tre vettori unitari.

Di solito l’origine del riferimento viene posta sul o nel corpo, ma questo non è assolutamente obbligatorio; possiamo collocare l’origine del riferimento anche fuori dal corpo, purchè lo segua nel suo moto, come se fosse idealmente “incollato” ad esso.

Ogni punto del corpo rigido può essere individuato (cioè si può dare la sua rappresentazione) nel sistema di riferimento appena stabilito, che chiameremo per semplicità sistema di riferimento corpo, in inglese body-frame. Ad esempio, se conosciamo il modello geometrico del corpo e le sue dimensioni, ogni punto è univocamente determinato utilizzando i vettori geometrici; così, in definitiva, stabilire il riferimento corpo è l’unica cosa necessaria per decriverne il moto del corpo stesso.

Non ho paura di ripetere che un vettore generico $\vvet$ nello spazio tridimensionale, sia esso un vettore geometrico o un vettore fisico, quando lo si rappresenta in coordinate cartesiane (e allora diciamo che il vettore “vive” nello spazio cartesiano), possiede tre componenti $v_1,v_2,v_3$ e lo si esprime così:

$$\vvet = v_1\ivet + v_2\jvet + v_3\kvet = \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array} \right]$$

Adesso ci chiediamo quale sia la rappresentazione dei tre vettori unitari $\ivet,\jvet,\kvet$ nel sistema di riferimento che loro stessi individuano. Nulla di più semplice: infatti applicando la formula precedente, avremo

$$\ivet=1\ivet + 0\jvet + 0\kvet= \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right] \\ \jvet=0\ivet + 1\jvet + 0\kvet= \left[\begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right] \\ \kvet=0\ivet + 0\jvet + 1\kvet= \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right]$$

Adesso organizziamo questi tre elementi mettendoli nella prima, nella seconda e nella terza colonna di una matrice, ottenendo perciò

$$\left[\begin{array}{c} \ivet & \jvet & \kvet \end{array} \right] =\left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right]= \Ivet$$

La matrice $\Ivet$ è la cosiddetta matrice identità, detta anche matrice unitaria. Possiamo concludere che un sistema di riferimento (e in generale qualunque sistema di riferimento), quando viene rappresentato in sè stesso, è caratterizzato - o meglio - è rappresentato dalla matrice identità.

Sistemi di Riferimento

Adesso procediamo. Come possiamo dire che un corpo è “qui” e non “lì”? Oppure calcolare qual’è la relazione tra due corpi posti in punti diversi con assetti diversi?

Vediamo la Figura sottostante, dove ci sono due teiere identiche.

Possiamo pensare a due situazioni alternative

1. Le due teiere sono oggetti distinti, ma identici, e sono poste in posizioni differenti con assetti differenti. Possiamo chiederci quali siano le relazioni che legano le due teiere, ad esempio, noto un punto sul beccuccio della teiera di destra, quale sia la rappresentazione rispetto alla teiera di sinistra, o qualcos’altro di simile.

2. Le due teiere sono la stessa teiera in due tempi distinti. Possiamo pensare, ad esempio, che la teiera di sinistra sia “fotografata” al tempo $t_0$ e la teiera di destra sia “fotografata” al tempo $t_1$. Nell’intervallo di tempo $\Delta t=t_1-t_0$ la teiera si è spostata da sinistra a destra e vogliamo ricostruirne (matematicamente) la storia del moto e la posizione finale.

Per affrontare questi problemi si procede così:

1. Fissiamo (idealmente) un sistema di riferimento sul corpo (in questo sulla teiera). Questo sistema di riferimento, come visto poco sopra è detto comunemente riferimento corpo e accompagna il corpo in ogni suo moto. Di solito lo indichiamo in modo esteso così:

$$\calR_B=(O_B,\ivet_B,\jvet_B,\kvet_B)$$

per mettere in evidenza la sua origine e i tre vettori unitari che compongono il riferimento. Spesso lo indichiamo più brevemente con $\calR_B$. Il pedice $B$ sta ad indicare il corpo su cui è fissato, perché indicarlo con $\calR_{\rm corpo}$, o con altre indicazioni più sbrodolate non è conveniente per chi scrive le formule. Altre volte, quando ci sono $N$ corpi, utilizziamo i simboli $\calR_1,\calR_2,\ldots\calR_N$, oppure usiamo dei pedici generici, come $\calR_A,\calR_B,\ldots\calR_Z$.

1. Fissiamo un riferimento, che chiameremo assoluto, rispetto al quale misurare il moto dei corpi. Nelle lezioni Fisica avrete sicuramente sentito parlare di sistema di riferimento inerziale, cioè di un riferimento che non è soggetto a moti accelerati di nessun genere.

Bene, un sistema di riferimento assoluto è praticamente un riferimento “quasi” inerziale (si dice tecnicamente che è pseudo-inerziale), nel senso che è sufficiente che le accelerazioni che agiscono su di esso siano trascurabili. Ad esempio il tavolo su cui state lavorando, se non viene mosso, può essere la sede di un sistema di riferimento assoluto, come nella foto che segue.

Infatti le uniche accelerazioni a cui è sottoposto sono quelle della rotazione della Terra intorno al suo asse e della rotazione della Terra intorno al Sole, che possiamo considerare entrambe trascurabili (per non parlare del moto del Sistema Solare rispetto alla nostra Galassia, e così via).

La Figura che segue rappresenta un sistema di riferimento pseudo-inerziale collocato sul mio tavolo di lavoro. I pennarelli colorati rappresentano i tre vettori unitari.

Il moto del corpo su cui è stato “incollato” il riferimento $\calR_B$ viene misurato in relazione al riferimento assoluto, che possiamo chiamare $\calR_0$.

Infatti sappiamo che il moto è sempre relativo a “qualcosa”; in questo caso al riferimento $\calR_0$.

Possiamo chiederci dove si collocano i due riferimenti. In teoria possiamo collocarli dove vogliamo, il primo in un punto che ha per noi qualche interesse e che non cambieremo nel corso del tempo, il secondo sul corpo di cui vogliamo studiare il moto.

In pratica il riferimento assoluto viene posto secondo le logiche dell’applicazione che vogliamo studiare. Nella robotica mobile, il riferimento assoluto si pone in qualche punto dell’ambiente che riteniamo importante, oppure nel punto iniziale del moto del robot. Il riferimento corpo si pone in una posizione che abbia qualche importanza per l’applicazione. Ad esempio, nei robot mobili a ruote differenziali la sua origine si pone al centro tra le due ruote con l’asse $x$ nella direzione di avanzamento, l’asse $y$ verso sinistra e l’asse $z$ rivolto verso l’alto.

Quindi, ricapitolando, abbiamo due riferimenti: $\calR_0$ che rimane immutabile nel corso del tempo e $\calR_B$ (o comunque lo si voglia chiamare) che segue l’oggetto che si muove. La Figura che segue presenta un esempio in tal senso, dove $\calR_0$ è il riferimento assoluto e $\calR_B$ è il riferimento sull’aeroplanino che mi muove.

Come si rappresenta matematicamente il movimento

Il movimento, come abbiamo anticipato, è composto da due sole “componenti” elementari: una traslazione e una rotazione, che possono combinarsi in una roto-traslazione.

Traslazioni

Supponiamo che inizialmente i due sistemi di riferimento, quello assoluto $\calR_0$, che potremmo anche chiamare riferimento zero e quello del corpo $\calR_B$, siano perfettamente coincidenti. Adesso immaginiamo che il secondo si sposti con un movimento di pura traslazione.

Il nuovo riferimento $\calR_B$ avrà i tre vettori unitari $(\ivet_B,\jvet_B,\kvet_B)$ paralleli a quelli del riferimento assoluto $(\ivet_0,\jvet_0,\kvet_0)$ , ma ora l’origine, che è individuata dal vettore $\ovet_B$, e che inizialmente valeva (nel riferimento $\calR_0$)

$\ovet_B= \left[ \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right]$ adesso sarà rappresentata del vettore (sempre nel riferimento $\calR_0$) $\ovet_B=\tvet= \left[ \begin{array}{c} t_1 \\ t_2 \\ t_3 \end{array} \right]$

dove $\tvet$ è il vettore che rappresenta la traslazione.

Esempio di traslazione

Nella Figura che segue sono indicati due sistemi di riferimento

Si possono dare due casi

1. se il sistema assoluto è quello di destra la traslazione è positiva lungo l’asse $x$ ed è pari a 20 cm, per cui $\tvet= \left[ \begin{array}{c} 0.20 \\ 0 \\ 0 \end{array} \right]\,\text{m}$

2. se il sistema assoluto è quello di sinistra la traslazione è negativa lungo l’asse $x$ ed è pari a 20 cm, per cui $\tvet= \left[ \begin{array}{c} -0.20 \\ 0 \\ 0 \end{array} \right]\,\text{m}$

###Combinazione di più traslazioni

Poichè la traslazione è rappresentata da un vettore e i vettori si possono sommare, e la somma è commutativa ($a+b=b+a$), allora ne segue che se eseguiamo più traslazioni in sequenza $\tvet_1,\tvet_2,\ldots,\tvet_N$ la traslazione totale è semplicemente la somma delle traslazioni, nell’ordine che si desidera: $\tvet_{\text{tot}} = \tvet_1 + \tvet_2 + \cdots + \tvet_N = \tvet_2 + \tvet_N + \cdots + \tvet_1$

Rotazioni

Immaginiamo di avere due sistemi di riferimento, che chiameremo $\calR_A$ e $\calR_B$, con l’origine in comune, ma orientati diversamente. Prendiamo ad esempio la Figura seguente, dove per ragioni di comprensibilità, le due origini sono state leggermente discostate.

Proviamo ora a rappresentare $\calR_A$ in $\calR_B$.

Il vettore unitario $\ivet_A$ è esattamente opposto al vettore unitario $\ivet_B$, quindi $\ivet_A=-1\ivet_B+0\jvet_B+0\kvet_B = \left[\begin{array}{c} -1 \\ 0 \\ 0 \end{array} \right]$

e così pure per gli altri vettori unitari, che risultano essere descritti come segue:

$\jvet_A=0\ivet_B+0\jvet_B+1\kvet_B = \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] \quad \quad \kvet_A=0\ivet_B+1\jvet_B+0\kvet_B = \left[\begin{array}{c} 0 \\ 1\\ 0 \end{array} \right]$ Creiamo la matrice, che chiamiamo $\Rvet^B_A$ dove la posizione degli indici ha questo significato: l’indice in basso individua qual’è il riferimento che si vuole rappresentare nel riferimento individuato dall’indice in alto, cioè $A$ rappresentato in $B.$ In fondo è una specie di differenza di potenziale, e si trovano nella letteratura scientifica altri modi per indicarla, ad esempio $^B\Rvet_A\quad\quad\Rvet_{AB}\quad\quad\Rvet_{BA}$ Io continuerò ad usare la notazione indicata, per cui si ha $\Rvet^B_A= \left[\begin{array}{ccc} -1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array} \right]$

Rappresentiamo ora la situazione duale, ciè rappresentiamo $\calR_B$ in $\calR_A$. Avremo $\ivet_B=-1\ivet_A+0\jvet_A+0\kvet_A = \left[\begin{array}{c} -1 \\ 0 \\ 0 \end{array} \right] \jvet_B=0\ivet_A+0\jvet_A+1\kvet_A = \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] \quad \quad \kvet_B=0\ivet_A+1\jvet_A+0\kvet_A = \left[\begin{array}{c} 0 \\ 1\\ 0 \end{array} \right]$ cioè $\Rvet^B_A= \left[\begin{array}{ccc} -1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array} \right]$

Le due matrici sono le stesse, e se applichiamo le proprietà raccontate nella soluzione dell’esercio 4.2, potete verificare che sono entrambe matrici ortonormali ovvero matrici di rotazione. Potete anche osservare che $\Rvet_A=\Rvet_B\T\quad \quad \Rvet_B=\Rvet_A\T$ e che - per combinazione - le due matrici sono identiche perché sono anche simmetriche. Non sempre questo fatto si verifica e non dobbiamo trarre conclusioni generali da questo fatto specifico.

Non abbiamo tempo ora, ma lo faremo nel prossimo post, di descrivere come sia stato possibile ottenere, attraverso delle rotazioni successive, il sistema di riferimento $\Rvet_A$ a partire da $\Rvet_B$ e viceversa

Conclusioni

1. Le traslazioni sono rappresentabili da vettori e sono operazioni commutative (si può cambiare l’ordine in cui sono eseguite)
2. Le rotazioni sono rappresentabili da matrici ortonormali (di rotazione) e NON sono operazioni commutative, cioè se si cambia l’ordine in cui cono eseguite cambia il risultato finale.

Riuscite a trovare l’ordine con cui si è potuto passare da $\Rvet_B$ a $\Rvet_B$?

Chi ne ha voglia mi mandi pure la soluzione per email.