Soluzione Esercizi Matrici e vettori - parte 4

---

Vediamo di risolvere i due esercizi proposti nel post precedente.

Esercizio 4.1

Sono dati tre punti $A,B,C$ e due vettori $\vvet_1, \vvet_2$, le cui componenti sono tutte rappresentate nello stesso sistema di riferimento nello spazio tridimensionale. Indichiamo con $\pvet_X$ il vettore geometrico che rappresenta il punto $X$. $\pvet_A= \left[ \begin{array}{c} 1 \\ 5 \\ 7 \end{array} \right]\; \pvet_B= \left[ \begin{array}{c} -3 \\ 8 \\ -2 \end{array} \right]\; \pvet_C= \left[ \begin{array}{c} 12 \\ 4 \\ -6 \end{array} \right]\; \vvet_1= \left[ \begin{array}{c} 1 \\ 8 \\ 4 \end{array} \right]\; \vvet_2= \left[ \begin{array}{c} 2 \\ 4 \\ 5 \end{array} \right]$

1. Calcolate le distanze di ciascun punto $A$, $B$ e $C$ dall’origine.
2. Dite quale sia la maggiore distanza reciproca tra i punti $A$, $B$ e $C$.
3. Ponete a zero la terza componente ($z=0$) dei punti $A$, $B$ e $C$, in modo da immaginare che i vettori stiano tutti sul piano base. Calcolate l’angolo tra $\vvet_1$ e $\vvet_2$ (suggerimento: il prodotto scalare tra due vettori vale $||\vvet_1||\cdot||\vvet_2||\cdot \cos \theta$ dove $\theta$ è l’angolo tra i vettori e il prodotto scalare si calcola come $\vvet_1\T \vvet_2$, cioè riga per colonna).
4. Disegnate su un foglio a quadretti i vettori del punto 3. e verificate di aver ottenuto l’angolo corretto.
5. Supponete che nel punto $A$ ci sia la massa di 1 kg. L’energia cinetica associata alla massa vale

$$\calK= \frac{1}{2}m ||\vvet||^2$$

dove $\vvet$ è la velocità totale della massa.

Quale delle due formule riportate qui sotto è quella corretta e perché?

$$\calK= \frac{1}{2}m ||\vvet_1+\vvet_2||^2\quad \text{ oppure }\quad\frac{1}{2}m (||\vvet_1||^2+||\vvet_2||^2)$$

Soluzione 4.1

Soluzione Domanda 1

Calcolate le distanze di ciascun punto $A$, $B$ e $C$ dall’origine.

Per calcolare la distanza di ciacun punto dall’origine è sufficiente ricordare che la distanza non è altro che la lunghezza del vettore, cioè la sua norma $||\cdot||$ e che la norma è la radice quadrata della somma dei quadrati delle tre componenti del vettore. Dunque

$$\begin{array}[l]\\ d(\overrightarrow{OA})=||\pvet_A||=\sqrt{1^2+5^2+7^2}=\sqrt{1+25+49}=\sqrt{75}\approx 8.66\\ d(\overrightarrow{OB})=||\pvet_B||=\sqrt{(-3)^2+8^2+(-2)^2}=\sqrt{9+64+4}=\sqrt{77}\approx 8.77\\ d(\overrightarrow{OC})=||\pvet_C||=\sqrt{12^2+4^2+(-6)^2}=\sqrt{144+16+36}=\sqrt{166}= 4 \end{array}$$

Si potrebbe obbiettare che la distanza potrebbe avere un segno: se si va da $O$ a $A$ si va nel verso positivo, se si va da $A$ ad $O$ si va nel verso negativo. L’obbiezione è corretta, perché si potrebbe (erroneamente) pensare che $d(\overrightarrow{OA})\neq d(\overrightarrow{AO})$. Attenzione però che la norma $||\cdot||$ fornisce sempre un numero maggiore o uguale a zero, e che $d(\overrightarrow{OA}) = d(\overrightarrow{AO})$ quindi per tenere conto del segno bisogna aggiungere un’informazione che non è “contenuta” nella norma.

Soluzione Domanda 2

Dite quale sia la maggiore distanza reciproca tra i punti $A$, $B$ e $C$.

Per calcolare la distanza reciproca dobbiamo calcolare la norma dei tre vettori $d(\overrightarrow{AB})$, $d(\overrightarrow{AC})$ e $d(\overrightarrow{BC})$.

Abbiamo visto che possiamo indicare il vettore tra due punti generici $X$ e $Y$ come $\overrightarrow{XY}$, che è rappresentato dalla freccia che va da $X$ a $Y$. La freccia opposta va da $Y$ a $X$ ed è data da $\overrightarrow{YX}$. Sappiamo anche che $\overrightarrow{XY}= Y-X$, cioè $\pvet_Y-\pvet_X$. Abbiamo visto sopra che la norma non dipende dal verso di percorrenza, quindi $||\pvet_X-\pvet_Y||=||\pvet_Y-\pvet_X||$ . Attenzione che invece usare la formula $||\pvet_X||-||\pvet_Y||$ è sbagliato.

In definitiva per rispondere alla domanda, dobbiamo calcolare $||\pvet_A-\pvet_B||$, $||\pvet_A-\pvet_C||$ e $||\pvet_B-\pvet_C||$

Prima calcoliamoci i vettori differenza $\pvet_A-\pvet_B=\left[\begin{array}{c} 1-(-3) \\ 5-8 \\ 7-(-2) \end{array}\right]=\left[\begin{array}{c} 4 \\ -3 \\ 9 \end{array}\right] \\ \pvet_A-\pvet_C=\left[\begin{array}{c} 1-12 \\ 5-4 \\ 7-(-6) \end{array}\right]=\left[\begin{array}{c} -11 \\ 1 \\ 13 \end{array}\right] \\ \pvet_B-\pvet_C=\left[\begin{array}{c} -3-12 \\ 8-4 \\ -2-(-6) \end{array}\right]=\left[\begin{array}{c} -15 \\ 4 \\ 4 \end{array}\right]$

Il risultato è $\begin{array}[l]\\ ||\pvet_A-\pvet_B||=\sqrt{4^2+(-3)^2+9^2}=\sqrt{16+9+81}=\sqrt{106}\approx 10.295\\ ||\pvet_A-\pvet_C||=\sqrt{(-11)^2+1^2+13^2}=\sqrt{121+1+169}=\sqrt{291}\approx 17.058\\ ||\pvet_B-\pvet_C||=\sqrt{(-15)^2+4^2+4^2}=\sqrt{225+16+16}=\sqrt{257}\approx 16.031 \end{array}$

Ora è immediato vedere quale sia la distanza maggiore.

Soluzione Domanda 3 e 4

Ponete a zero la terza componente ($z=0$) dei punti $A$, $B$ e $C$, in modo da immaginare che i vettori stiano tutti sul piano base. Calcolate l’angolo tra $\vvet_1$ e $\vvet_2$.

Ricordiamo che il prodotto scalare tra due vettori $\avet$ e $\bvet$ è una grandezza scalare, che soddisfa a questa proprietà $\avet\T\bvet=||\avet||\;||\bvet||\cos(\theta)$ dove il simbolo $\T$ indica il vettore trasposto, cioè da vettore colonna a vettore riga. Quindi possiamo ricavare l’angolo con la funzione inversa del coseno, come $\theta=\arccos\frac{\avet\T\bvet}{||\avet||\;||\bvet||}$

L’angolo tra i vettori $\vvet_1$ e $\vvet_2$ dopo che la terza componente è stata posta a zero, vale quindi $\vvet_1\T\vvet_2=\left[\begin{array}{c} 1 & 8 & 0 \end{array}\right]\left[\begin{array}{c} 2 \\ 4 \\ 0 \end{array}\right]=1\times2+8\times 4=34$ e $||\vvet_1||\approx 8.062\quad \quad ||\vvet_2||\approx 4.472$ da cui $\theta\approx\arccos\frac{34}{8.062\times 4.472}= \arccos(0.9430)=0.3391$ L’angolo $\theta$ è espresso in radianti e per convertirlo in gradi dobbiamo moltiplicarlo per la costante $180/\pi\approx 57.296$. Il risultato in gradi risulta pertanto $\theta\approx 19.43$. Se qualcuno possiede ancora un goniometro, può verificare il risultato disegnando i due vettori su un foglio di carta, come ho fatto io qui sotto

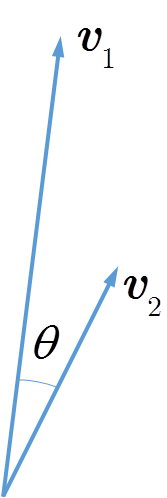
Soluzione Domanda 5

Supponete che nel punto $A$ ci sia la massa di 1 kg. L’energia cinetica associata alla massa vale $\calK= \frac{1}{2}m ||\vvet||^2$ dove $\vvet$ è la velocità totale della massa. Quale delle due formule riportate qui sotto è quella corretta e perché? $\calK= \frac{1}{2}m ||\vvet_1+\vvet_2||^2\quad \text{ oppure }\quad\frac{1}{2}m (||\vvet_1||^2+||\vvet_2||^2)$

La soluzione corretta è la prima, perché per calcolare la velocità totale della massa occorre prima sommare i due vettori e poi calcolare la norma del vettore risultante.

---

Esercizio 4.2

Ed ora affrontiamo il secondo esercizio, che diceva:

Prendete il vettore $\vvet=\left[\begin{array}{c} -3 \ 8 \ -2 \end{array}\right]$ e due matrici $\Rvet_1= \left[ \begin{array}{ccc} 0 & 0 & -1
-1 & 0 & 0
0 & 1 & 0 \end{array} \right]$ e $\Rvet_2=\left[ \begin{array}{ccc} 0 & 0.707 & 0.707
0 & 0.707 & -0.707
-1 & 0 & 0 \end{array} \right]$ dove $0.707 \approx \frac{\sqrt 2}{2}$.

Fate i seguenti prodotti $\vvet_1 = \Rvet_1\vvet, \quad \vvet_2 = \Rvet_2 \vvet, \quad \vvet_3 = \Rvet_1\Rvet_2 \vvet$ per ottenere i tre vettori $\vvet_1,\vvet_2,\vvet_3$.

Adesso confrontate la norma di $\vvet$ con le norme dei tre nuovi vettori. Cosa notate? Sono tutte uguali. Nonostante $\vvet$ sia stato “trasformato” dal prodotto di matrice, la sua norma non cambia. Sarà per caso “merito” della struttura delle matrici $\Rvet$?

Soluzione 4.2

Eseguiamo per prima cosa i prodotti indicati, ricordandoci della regola del prodotto tra matrici (infatti anche un vettore è una matrice con una sola colonna):

$$\Mvet\vvet=\left[ \begin{array}{ccc} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{array} \right]\; \left[ \begin{array}{c} x_1\\x_2\\x_3 \end{array} \right]= \left[ \begin{array}{c} m_{11}x_1+m_{12}x_2+m_{13}x_3\\ m_{21}x_1+m_{22}x_2+m_{23}x_3\\ m_{31}x_1+m_{32}x_2+m_{33}x_3 \end{array} \right]$$

Nel nostro caso avremo

$$\vvet_1= \Rvet_1\vvet= \left[ \begin{array}{ccc} 0 & 0 & -1 \\ -1 & 0 & 0 \\ 0 & 1 & 0 \end{array} \right] \left[ \begin{array}{c} -3 \\ 8 \\ -2 \end{array} \right]= \left[ \begin{array}{c} 2\\ 3\\ 8 \end{array} \right]$$ $$\vvet_2= \Rvet_2\vvet= \left[ \begin{array}{ccc} 0 & 0.707 & 0.707 \\ 0 & 0.707 & -0.707 \\ -1 & 0 & 0 \end{array} \right]\left[\begin{array}{c} -3 \\ 8 \\ -2 \end{array}\right]= \left[ \begin{array}{c} 4.24\\ 7.07\\ 3 \end{array} \right]$$ $$\vvet_3= \Rvet_1\Rvet_2\vvet= \left[ \begin{array}{ccc} 0 & 0 & -1 \\ -1 & 0 & 0 \\ 0 & 1 & 0 \end{array} \right] \left[ \begin{array}{ccc} 0 & 0.707 & 0.707 \\ 0 & 0.707 & -0.707 \\ -1 & 0 & 0 \end{array} \right] \left[\begin{array}{c} -3 \\ 8 \\ -2 \end{array}\right]= \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & -0.707 & -0.707 \\ 0 & 0.707 & -0.707 \end{array} \right] \left[\begin{array}{c} -3 \\ 8 \\ -2 \end{array}\right] =\left[ \begin{array}{c} -3\\ -4.24\\ 7.07 \end{array} \right]$$

I risultati sono approssimati alla seconda cifra decimale.

Nota: tutti i calcoli sono stati fatti utilizzando il package MATLAB, ma chi non avesse la licenza potrebbe utilizzare in alternativa Octave oppure SCILAB, entrambi open-source.

Ora vediamo di scoprire qualche caratteristica dei vettori così ottenuti.

In primo luogo notiamo che le norme di tutti i vettori sono identiche, a parte le approssimazioni introdotte nei calcoli. $||\vvet||=||\vvet_1||=||\vvet_2||=||\vvet_3||=8.775$

Possiamo quindi dire che essi sono stati “trasformati” dalle matrici $\Rvet$, ma la lora norma resta invariata. A cosa è dovuto questo fatto? Per rispondere esaminiamo le caratteristice delle matrici $\Rvet$.

Proviamo a calcolare il determinante di ciascuna matrice. Per calcolare il determinante si può ricorrere ai package indicati sopra, oppure farlo a mano. Non entrerò nei dettagli circa la regola per calcolarsi il determinante, che si può trovare ovunque sul web.

Vediamo che tutti i determinanti sono uguali a $+1$, a parte le approssimazioni introdotte nei calcoli. $det(\Rvet_1)=det(\Rvet_1)=det(\Rvet_3)=+1$

dove $\Rvet_3=\Rvet_1\Rvet_2$.

Inoltre tutte le righe e le colonne delle matrici hanno norma unitaria.

In terzo luogo, ogni riga e ogni colonna delle matrici è ortogonale ad ogni altra riga o colonna. L’ortogonalità consiste nell’avere l’angolo $\theta$ tra i vettori uguale a 90 gradi, cioè il $cos(\theta)=0$, il che vuole anche dire che il prodotto scalare è uguale a zero.

E, da ultimo, ma non meno importante, che il prodotto di ogni matrice $\Rvet$ per la sua trasposta, dà la matrice identità $\Rvet_1\T\Rvet_1=\Rvet_1\Rvet_1\T=\Ivet; \quad \Rvet_2\T\Rvet_2=\Rvet_2\Rvet_2\T=\Ivet; \quad \Rvet_3\T\Rvet_3=\Rvet_3\Rvet_3\T=\Ivet$ Tecnicamente questa proprietà significa che l’inversa di queste matrici $\Rvet$ coincide esattamente con la loro trasposta, cioè $\Rvet^{-1}=\Rvet\T$

Queste matrici sono dette matrici di rotazione, cioè matrici che rappresentano le rotazioni nello spazio tridimensionale.

Esistono anche altre matrici che hanno tutte le proprietà elencate sopra tranne quella del determinante, che per loro vale $-1$. Queste matrici, dette matrici di riflessione, non le consideriamo proprio, anche se hanno un significato geometrico ben preciso.

Conclusioni

L’ultimo esercizio ci ha permesso di scoprire che esistono delle matrici con particolari proprietà, che quando moltiplicano (cioè “trasformano”) i vettori, non modificano la loro norma, che hanno righe e colonne unitarie, che hanno righe e colonne ortogonali tra loro, che hanno determinante positivo unitario e la cui inversa coincide con la trasposta.

Sono le matrici di rotazione.

Vedremo come si possono usare queste matrici di rotazione per rappresentare i corpi rigidi nello spazio e i loro moti di rotazione.

Arrivederci alla prossima puntata.