Matrici e vettori - parte 4

$$\def\ivet{\boldsymbol{i}} \def\jvet{\boldsymbol{j}} \def\kvet{\boldsymbol{k}} \def\avet{\boldsymbol{a}} \def\bvet{\boldsymbol{b}} \def\cvet{\boldsymbol{c}} \def\fvet{\boldsymbol{f}} \def\vvet{\boldsymbol{v}} \def\pvet{\boldsymbol{p}} \def\omvet{\boldsymbol{\omega}} \def\tauvet{\boldsymbol{\tau}} \def\Rvet{\boldsymbol{R}} \def\calK{\mathcal{K}} \def\calP{\mathcal{P}} \def\calR{\mathcal{R}} \def\de{\textrm{d}}$$

Dopo un lungo periodo di silenzio, riprendo a scrivere, dedicandomi a iniziare a spiegarvi quanto vi avevo promesso nell’ultimo post pubblicato:

• Come si trasformano i vettori passando da un riferimento ad un altro?
• Come si rappresenta l’orientamento angolare di un corpo rigido?
• Come si rappresentano i movimenti di un corpo rigido?

Riassunto delle puntate precedenti

Do per scontato che vi ricordiate qualcosa del calcolo vettoriale; infatti lo scopo di questo post non è di spiegare da zero cosa sono i vettori, ma come si trasformano le loro componenti passando da un riferimento all’altro. Chi non si ricorda qualcosa può sempre interrogare il web, che è ricco di corsi sui vettori e le matrici.

Ricapitoliamo quello che abbiamo imparato nei post precedenti:

1. Un punto è descritto da un vettore geometrico che rappresenta lo spostamento dall’origine di un sistema di riferimento al punto stesso. Da un punto (scusate il bisticcio) di vista “metafisico” un punto esiste indipendentemente dalla presenza di un sistema di riferimento, ma se vogliamo darne una rappresentazione, ci dobbiamo sobbarcare la presenza di un sistema di riferimento (cartesiano e destro, ricordate). Quindi il punto è visto come spostamento e la freccia (cioè l’icona usata per rappresentare il vettore) ci rappresenta appunto questo spostamento.

2. Una grandezza fisica (come una forza o una velocità) caratterizzata da un modulo (la sua “grandezza”), una direzione e un verso, è rappresentata anch’essa da un vettore fisico, ma i due tipi di vettore sono diversi, come vedremo poi quando dobbiamo trasformarli passando da un riferimento ad un altro. Anche qui le grandezze vettoriali esistono indipendentemente da ogni sistema di riferimento (quando battete la testa e il muro esercita una forza impulsiva sulla vostra fronte, non vi ponete il problema della presenza di un sistema di riferimento in cui rappresentare la forza). Però se è necessario quantificare e individuare la direzione e il verso della forza vi occorre avere un sistema di riferimento.

3. Possiamo sommare tra loro due vettori fisici, ma non possiamo sommare due punti (cioè possiamo farlo, non è che caschi il mondo, ma il risultato non ha nessun senso). Possiamo invece sottrarre due punti e quello che si ottiene è un vettore che li “collega”. Potremo perciò dire che un punto geometrico è la differenza tra il punto stesso $P$ e il punto che rappresenta l’origine $O$ del sistema di riferimento che stiamo utilizzando.

4. I vettori, nello spazio tridimensionale sono definiti da una terna di numeri, di solito posta in colonna, I numeri sono detti componenti del vettore, rispetto ad un sistema di riferimento che definiamo a piacer nostro; quindi: $\vvet= \left[ \begin{array}{l} v_1 \\ v_2 \\ v_3 \end{array} \right] \text{ Ad esempio, } \vvet=\left[ \begin{array}{l} -\pi \\ 72.5 \\ -\sqrt{2} \end{array} \right]$ la cui norma vale $||\vvet|| =\sqrt{\pi^2+72.5^2+2}\approx \sqrt{5268.1}$.

Esempio

Nella figura qui sotto abbiamo un sistema di riferimento con l’origine nel punto $O$. Poi immaginiamo due punti $P$ e $Q$ e il vettore fisico $\vvet_1$, che rappresenta una velocità applicata nel punto $A$ ed un’altra velocità $\vvet_2$ applicata nello stesso punto $A$. Insomma, il punto $A$ è soggetto a due velocità per cause che non ci interessa indagare ora.

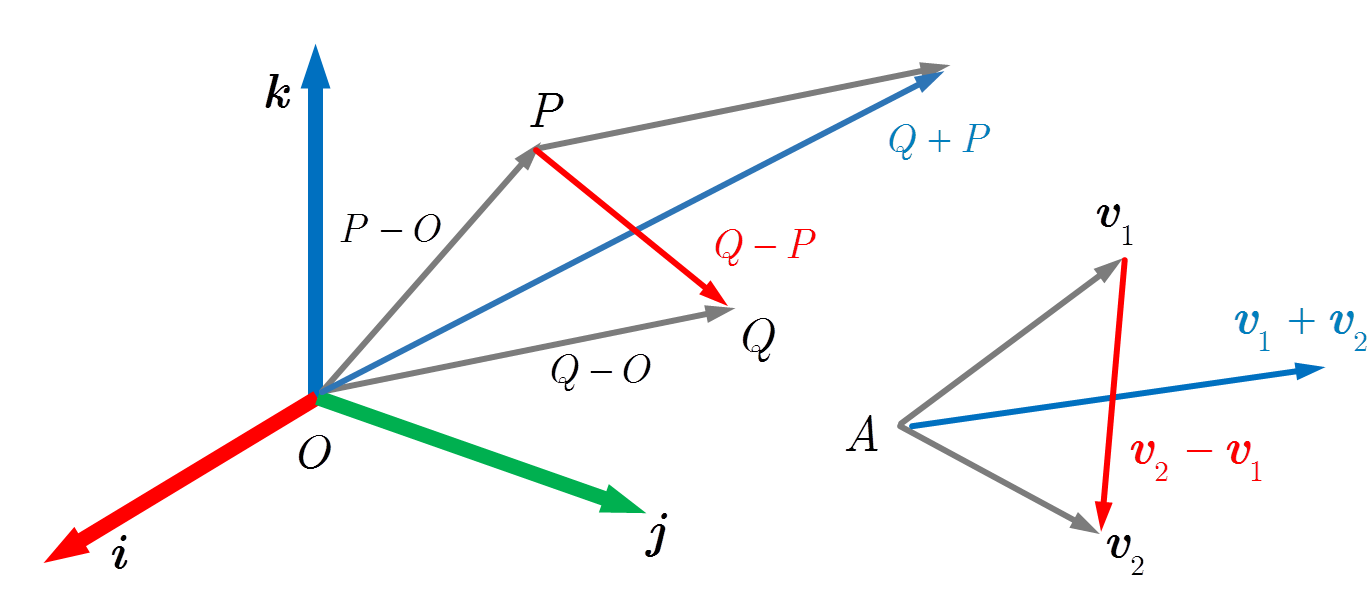
Cosa possiamo dire?

• Il vettore $\overrightarrow{OP}$ rappresenta il punto geometrico $P$, ed è la differenza $P-O$ tra due punti ($P$ e l’origine $O$).

• Lo stesso si può dire del punto geometrico $Q$, cioè anch’esso è rappresentato dalla differenza $\overrightarrow{OQ}=Q-O$

• Se proviamo a sommare $P+Q$ (cosa che si può fare), non otteniamo nulla di significativo (più avanti, quando parleremo della cinematica del robot la somma di punti geometrici avrà un senso, ma per ora lasciamo perdere).

• Invece $Q-P=\overrightarrow{PQ}$ è il vettore di spostamento per andare da $P$ a $Q;$ analogamente l’inverso $P-Q=\overrightarrow{QP}$ è il vettore di spostamento per andare da $Q$ a $P$.

• Se sommiamo i due vettori $\vvet_1$ e $\vvet_2$ otteniamo un terzo vettore $\vvet=\vvet_1+\vvet_2$ e questo ha un significato fisico ben preciso: rappresenta la velocità totale a cui è soggetto il punto $A$.

Adesso vediamo come si trasformano questi benedetti vettori: per fare questo è necessario capire come si rappresentano i sistemi di riferimento, introducendo le matrici di rotazione.

Ma questo lo capiremo nel prossimo post, abbiate pazienza. Ora vi sottopongo qualche esercizio, che dovrete cercare di risolvere per vedere se avete capito.

Se avete dubbi o domande, chiedete pure.

Esercizio 4.1

Sono dati tre punti $A,B,C$ e due vettori $\vvet_1, \vvet_2$, le cui componenti sono tutte rappresentate nello stesso sistema di riferimento nello spazio tridimensionale. Indichiamo con $\pvet_X$ il vettore geometrico che rappresenta il punto $X$. $\pvet_A= \left[ \begin{array}{c} 1 \\ 5 \\ 7 \end{array} \right]\; \pvet_B= \left[ \begin{array}{c} -3 \\ 8 \\ -2 \end{array} \right]\; \pvet_C= \left[ \begin{array}{c} 12 \\ 4 \\ -6 \end{array} \right]\; \vvet_1= \left[ \begin{array}{c} 1 \\ 8 \\ 4 \end{array} \right]\; \vvet_2= \left[ \begin{array}{c} 2 \\ 4 \\ 5 \end{array} \right]$

1. Calcolate le distanze di ciascun punto $A$, $B$ e $C$ dall’origine.
2. Dite quale sia la maggiore distanza reciproca tra i punti $A$, $B$ e $C$.
3. Ponete a zero la terza componente ($z=0$) dei punti $A$, $B$ e $C$, in modo da immaginare che i vettori stiano tutti sul piano base. Calcolate l’angolo tra $\vvet_1$ e $\vvet_2$ (suggerimento: il prodotto scalare tra due vettori vale $||\vvet_1||\cdot||\vvet_2||\cdot \cos \theta$ dove $\theta$ è l’angolo tra i vettori e il prodotto scalare si calcola come $\vvet_1^T \vvet_2$, cioè riga per colonna).
4. Disegnate su un foglio a quadretti i vettori del punto 3. e verificate di aver ottenuto l’angolo corretto.
5. Supponete che nel punto $A$ ci sia la massa di 1 kg. L’energia cinetica associata alla massa vale

dove $\vvet$ è la velocità totale della massa.

Quale delle due formule riportate qui sotto è quella corretta e perché?

Esercizio 4.2

Prendete il vettore $\vvet=\left[\begin{array}{c} -3 \ 8 \ -2 \end{array}\right]$ e due matrici
$\Rvet_1=\left[ \begin{array}{ccc} 0 & 0 & -1 \\ -1 & 0 & 0 \\ 0 & 1 & 0 \end{array} \right]$ e $\Rvet_2=\left[ \begin{array}{ccc} 0 & 0.7071 & 0.7071 \\ 0 & 0.7071 & -0.7071 \\ -1 & 0 & 0 \end{array} \right]$ dove $0.7071 \approx \frac{\sqrt 2}{2}$.

Fate i seguenti prodotti $\vvet_1 = \Rvet_1\vvet, \quad \vvet_2 = \Rvet_2 \vvet, \quad \vvet_3 = \Rvet_1\Rvet_2 \vvet$ per ottenere i tre vettori $\vvet_1,\vvet_2,\vvet_3$.

Adesso confrontate la norma di $\vvet$ con le norme dei tre nuovi vettori. Cosa notate? Sono tutte uguali. Nonostante $\vvet$ sia stato “trasformato” dal prodotto di matrice, la sua norma non cambia. Sarà per caso “merito” della struttura delle matrici $\Rvet$?

Infatti è così.

Provate a scoprire quali siano le caratteristiche strutturali delle due matrici e poi ne riparliamo in uno dei prossimi post.

Buon lavoro e a risentirci presto.