Matrici e vettori - parte 3

$$\def\ivet{\boldsymbol{i}} \def\jvet{\boldsymbol{j}} \def\kvet{\boldsymbol{k}} \def\avet{\boldsymbol{a}} \def\bvet{\boldsymbol{b}} \def\cvet{\boldsymbol{c}} \def\fvet{\boldsymbol{f}} \def\vvet{\boldsymbol{v}} \def\pvet{\boldsymbol{p}} \def\omvet{\boldsymbol{\omega}} \def\tauvet{\boldsymbol{\tau}} \def\Rvet{\boldsymbol{R}} \def\calR{\mathcal{R}} \def\de{\textrm{d}}$$

Come promesso nell’ultimo post prima delle vacanze estive, vi parlerò dei vettori fisici e delle due diverse tipologie di questi: i vettori polari e i vettori assiali.

#Vettori Fisici

Cosa intendo per vettori fisici? Sono quei vettori che rappresentano matematicamente le grandezze fisiche che possono tornare utili alla rappresentazione della cinematica e della dinamica dei robot.

Ci sono molti tipi di grandezze fisiche; alcune non sono rappresentabili come vettori.

Ad esempio, la temperatura è una grandezza fisica scalare perché non ha una direzione e un verso, ma solo un’intensità.

Altre invece sono dotate di intensità, direzione e verso e quindi sono grandezze vettoriali; in robotica se ne utilizzano relativamente poche:

1. velocità lineari, che indichiamo con il simbolo $\vvet$
2. accelerazioni lineari, che indichiamo con il simbolo $\avet$ oppure con $\dot{\vvet}$
3. velocità angolari, che indichiamo con il simbolo $\omvet$
4. accelerazioni angolari, che indichiamo con il simbolo $\dot\omvet$
5. forze lineari, che indichiamo con il simbolo $\fvet$
6. forze angolari, dette anche coppie o momenti , che indichiamo con il simbolo $\tauvet$

Le velocità lineari sono le derivate delle coordinate di posizione (vettori geometrici) dei punti materiali che ci interessano, mentre le velocità angolari sono le derivate delle coordinate angolari dei sistemi di riferimento che ci interessano. Parleremo diffusamente delle coordinate angolari in un post dedicato alla rappresentazione delle rotazioni.

Ad esempio, nella Figura seguente troviamo un sistema di riferimento $(O,\ivet,\jvet,\kvet)$ (destrorso, come sempre), una massa $m$ collocata in un punto geometrico rappresentato dal vettore geometrico $\pvet$ che possiede una velocità $\vvet$ e su cui agisce una forza esterna $\fvet$.

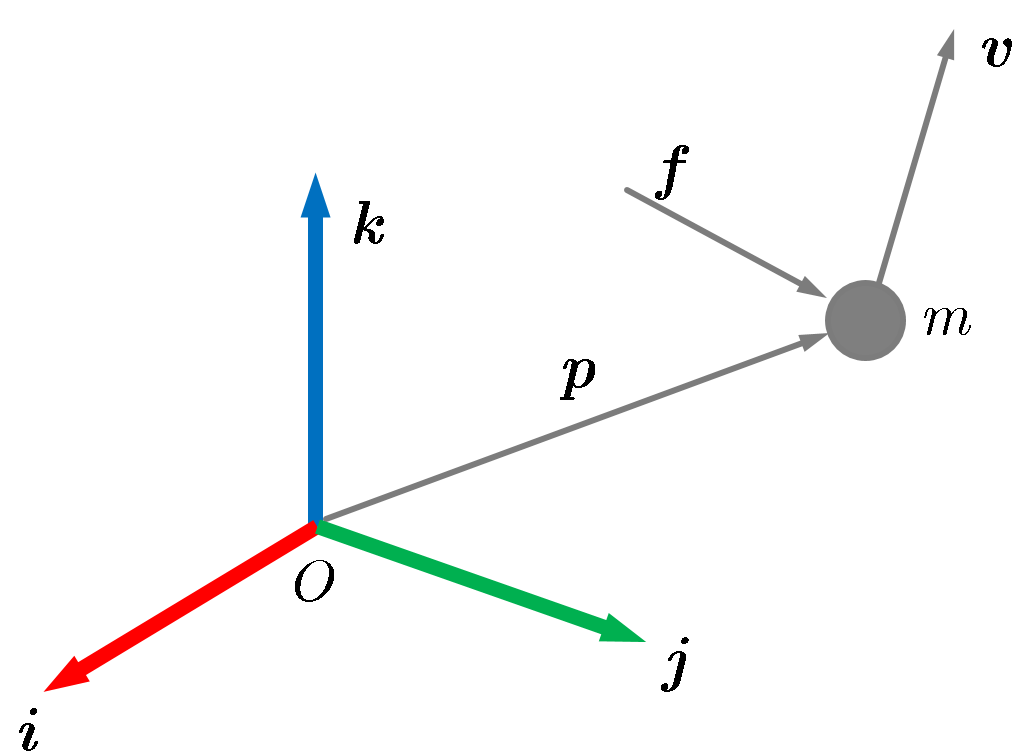
Facciamo ora una piccola parentesi. In robotica è importante lo studio della cinematica, ma anche quello della dinamica. Nella cinematica ci occupiamo solo del problema di stabilire le posizioni e le velocità (lineari e/o angolari) di punti particolari del robot, come la punta operativa o i centri di massa dei vari bracci; escludiamo perciò l’interazione con le forze, che invece sono importanti nello studio della dinamica, che appunto studia la relazione tra forze applicate e accelerazioni risultanti. Ricordiamo la famosissima Legge di Newton che stabilisce la seguente identità (vettoriale) $\fvet=m\avet = m\dot\vvet = \dfrac{\de \vvet}{\de t} = m \ddot \pvet = \dfrac{\de^2\pvet}{\de t^2}$

che lega le forze alle accelerazioni agenti su una massa (o viceversa).

Per il momento lasciamo da parte la dinamica e focalizziamoci sulla cinematica, dove utilizziamo solo le grandezze vettoriali elencate sopra dalla 1. alla 4. con l’esclusione appunto delle forze lineari e angolari.

Tutti i vettori fisici sono rappresentati graficamente da frecce, perché possiedono intensità (il modulo o norma del vettore), direzione e verso, ma queste frecce sono un’icona ambigua perché non distinguono tra vettori polari e vettori assiali. Bisognerebbe usare due tipi diversi di icone, come quelle indicata qui sotto

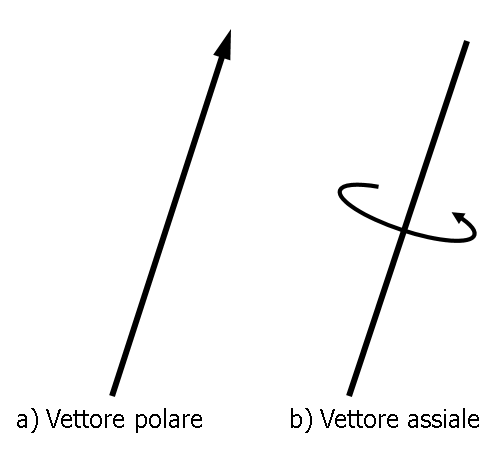
A sinistra l’icona del vettore polare, che è la solita freccia, mentre a destra c’è la proposta per un’icona del vettore assiale, che potrebbe essere un segmento intorno a cui si chiude un ricciolo con una freccia.

Purtroppo l’icona “ricciolo” per il vettore assiale non viene (quasi) mai usata e allora bisogna fare attenzione alla diversa interpretazione della stessa icona “freccia”.

Insomma, quali sono le caratteristiche di questi due tipi di vettore?

Vettori polari

Questi sono caratterizzati da essere invarianti (ovvero le loro caratteristiche non cambiano) quando vengono riflessi rispetto ad un piano parallelo al vettore, cioè il piano $P_1$ della Figura, mentre invece cambiano verso quando sono riflessi rispetto ad un piano perpendicolare al vettore (il piano $P_2$ della Figura). Nel caso illustrato si avrebbe

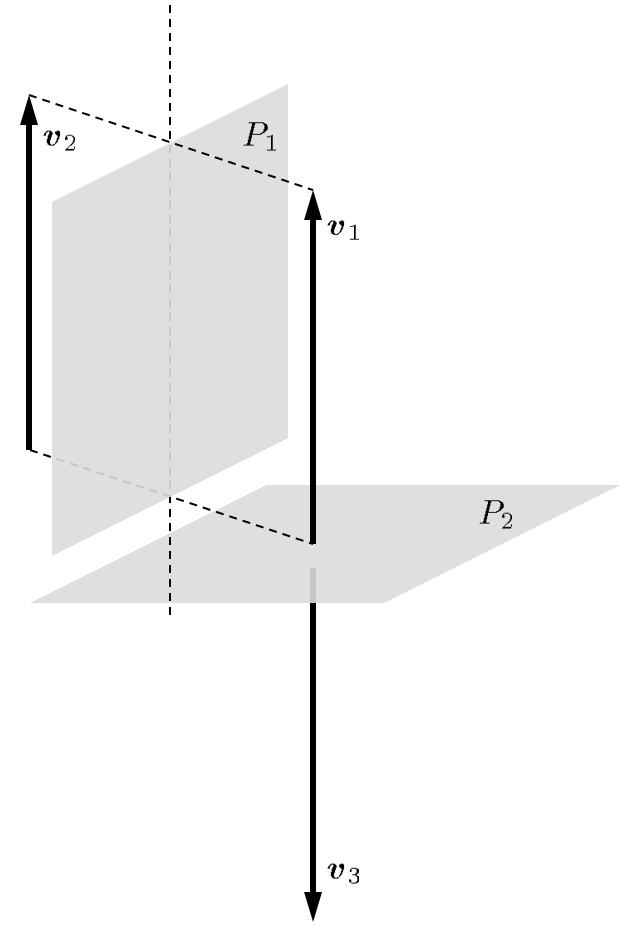
Esempi di vettori polari sono quelli relativi a grandezze fisiche come le posizioni, le velocità e le accelerazioni lineari, le forze lineari e molti altri che al momento non interessano per lo studio della cinematica dei robot.

##Vettori Assiali

Questi sono chiamati anche pseudovettori e sono caratterizzati da proprietà di invarianza rispetto alle riflessioni, ma in modo diverso dai vettori polari.

Chi fosse interessato, può leggere la voce pseudovettore (in inglese) su Wikipedia.

Prima di procedere è necessario trasformare idealmente l’icona “freccia” del vettore assiale nell’icona “ricciolo”, come illustrato qui sotto

Come si vede, utilizziamo la regola della mano destra per passare dalla direzione/verso della freccia, lungo cui sia allinea il pollice della mano destra, al ricciolo, che è raffigurato dalle altre dita della mano destra.

Fatto questo, possiamo rappresentare le simmetrie e le antisimmetrie del vettore assiale. Facendo riferimento alla Figura seguente

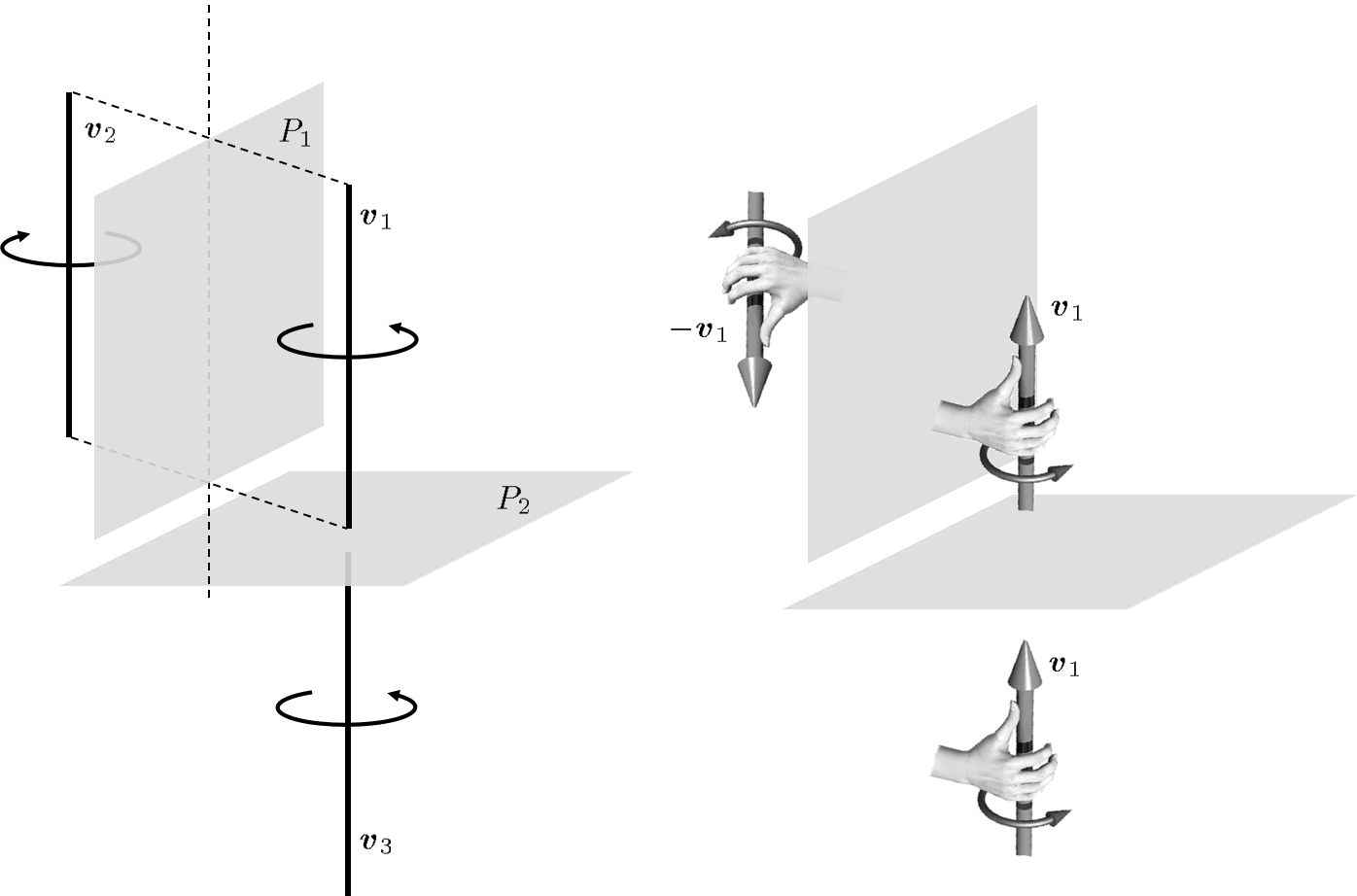
vediamo che il vettore assiale cambia il verso del ricciolo (antisimmetria) se lo si riflette rispetto ad un piano parallelo al vettore stesso, mentre il verso del ricciolo non cambia (simmetria) se lo si riflette rispetto ad un piano perpendicolare al vettore stesso.

Nel caso illustrato si avrebbe dunque

Esempi di vettori assiali sono quelli relativi a grandezze fisiche come gli angoli, le velocità e le accelerazioni angolari, le forze angolari e altri nell’ambito dell’elettromagnetismo, che al momento non interessano per lo studio della cinematica dei robot.

Per essere precisi, gli angoli che definiscono l’orientamento di un corpo e che spiegherò diffusamente in un prossimo post, non possono essere definiti come vettori (mentre ad esempio le posizioni sono vettori a tutti gli effetti) per una ragione matematica che al momento non vi spiego.

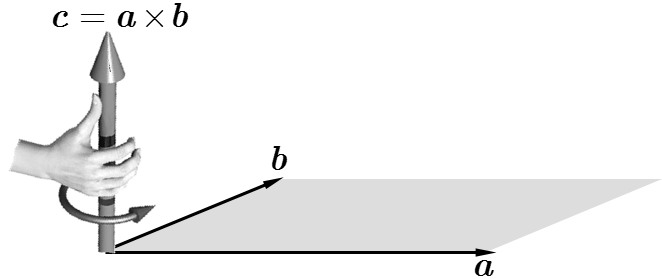
Un altro esempio di vettore assiale che viene spesso considerato nella cinematica è quello che risulta da un prodotto vettoriale tra due vettori polari $\avet$ e $\bvet$: $\cvet=\avet \times\bvet$

Ci ricordiamo che il vettore $\cvet$ ha un modulo pari all’area del parallelogramma definito dai lati $\avet$ e $\bvet$, direzione ortogonale al piano formato da $\avet$ e $\bvet$, e verso ottenuto applicando la regola della mano destra, che fa ruotare $\avet$ fino a soprapporsi alla direzione di $\bvet$ secondo il minore dei due angoli possibili (nel nostro caso il verso orario).

##Vettori fisici e sistemi di riferimento##

Nel post dove descrivevo i vettori geometrici, avevo spiegato come un generico vettore, rappresentato dalle sue componenti in un sistema di riferimento, viene successivamente rappresentato in un altro sistema di riferimento, non solo cambiano le sue componenti, ma anche il modulo subisce una variazione.

Questo invece non accade per i vettori fisici: ad esempio, una velocità in un sistema di riferimento non cambia il suo modulo se la si rappresenta in un sistema di riferimento diverso, ma cambia solo il valore delle sue componenti.

Cioè, dato il vettore fisico (polare oppure assiale) $\vvet_A$ rappresentato nel riferimento $\calR_A$ e lo stesso vettore chiamato $\vvet_B$ quando viene rappresentato nel riferimento $\calR_B$, si avrà $\vvet_A=\left( \begin{array}{c} v_{A,1}\\ v_{A,2} \\ v_{A,3} \end{array}\right) \neq\vvet_B=\left( \begin{array}{c} v_{B,1}\\ v_{B,2} \\ v_{B,3} \end{array}\right)$ ma $|\vvet_A|=\sqrt{v_{A,1}^2+v_{A,2}^2+v_{A,3}^2}=|\vvet_B|=\sqrt{v_{B,1}^2+v_{B,2}^2+v_{B,3}^2}$

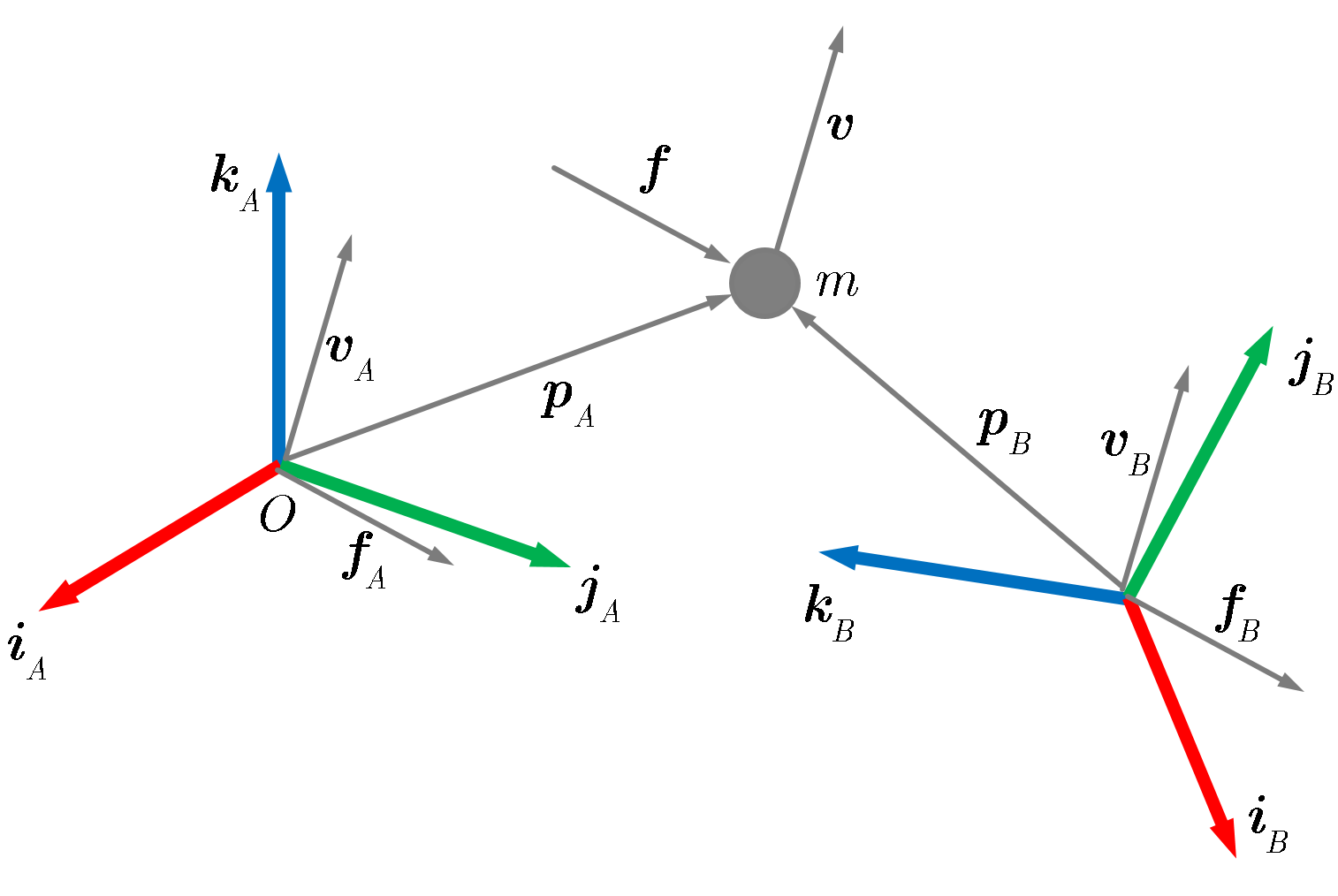
Nella Figura che segue ho disegnato una massa $m$ la cui posizione è data da due vettori geometrici $\pvet_A$ e $\pvet_B$ nei due riferimenti $\calR_A$ e $\calR_B$. Come si vede i loro moduli sono diversi.

Invece i vettori fisici velocità $\vvet$ e forza $\fvet$, hanno componenti diverse nei due riferimento, ma lo stesso modulo.

##Conclusioni##

Abbiamo dunque imparato a distinguere i vettori polari da quelli assiali, e abbiamo imparato che i vettori fisici quando vengono rappresentati in riferimenti diversi non cambiano il modulo.

Adesso possediamo quasi tutti gli elementi per procedere nello studio della cinematica di un robot; ci mancano solo le risposte ad alcune domande:

1. Come si trasformano i vettori passando da un riferimento ad un altro?
2. Come si rappresenta l’orientamento angolare di un corpo rigido?
3. Come si rappresentano i movimenti di un corpo rigido?

Nei prossimi post cercherò di rispondere a queste domande.

Scrivetemi, se avete dei dubbi.