$$ \def\ivet{\boldsymbol{i}} \def\jvet{\boldsymbol{j}} \def\kvet{\boldsymbol{k}} \def\avet{\boldsymbol{a}} \def\bvet{\boldsymbol{b}} \def\cvet{\boldsymbol{c}} \def\fvet{\boldsymbol{f}} \def\ovet{\boldsymbol{o}} \def\pvet{\boldsymbol{p}} \def\tvet{\boldsymbol{t}} \def\uvet{\boldsymbol{u}} \def\vvet{\boldsymbol{v}} \def\omvet{\boldsymbol{\omega}} \def\tauvet{\boldsymbol{\tau}} \def\Ivet{\boldsymbol{I}} \def\Mvet{\boldsymbol{M}} \def\Rvet{\boldsymbol{R}} \def\calK{\mathcal{K}} \def\calP{\mathcal{P}} \def\calR{\mathcal{R}} \def\de{\textrm{d}} \def\T{^{\sf T}} $$

Matrici e vettori - parte 1

By Basilio Bona on July 10, 2017

Matrici e vettori

Cari affezionatissimi lettori, forse questo post risulterà alla fine un po’ indigesto, ma vi chiedo di essere pazienti, perché alla fine tutto questo vi sarà utile.

Da parte mia farò il possibile per essere chiaro e spiegare le ragioni per cui introduco certi concetti e insisto su questo o quel particolare. Non sono un sadico, ma se volete essere a conoscenza degli intimi segreti della robotica, dovrete fare un piccolo sforzo.

Infatti, per capire la cinematica inversa dei robot, soprattutto quelli industriali, è necessario prima capire che cos’è la cinematica diretta, ma per capire come scrivere le equazioni della cinematica diretta, occorre conoscere principalmente alcune cose:

  1. Cosa sono i sistemi di riferimento: facile; probabilmente sapete già tutto, ma un ripassìno non porta via molto tempo ed è utile.

  2. Cosa sono i vettori, ma, soprattutto come si usano e come si devono interpretare. Forse pensate che sia tempo perso, perché anche qui sapete già tutto, ma vi assicuro che la mia esperienza di insegnamento ultra trentennale mi fa dire che così non è … e poi ci sono i quaternioni alla fine del percorso … yum yum!

  3. Cosa sono e come si usano le matrici di rotazione. Anche tutti gli altri tipi di matrice sono importanti, ma in robotica le matrici di rotazione sono un must, un po’ come per uno chef è indispensabile saper fare un ottimo riso all’inglese (o all’olio se siete vegani).

  4. Le basi della trigonometria. Basta ricordarsi cosa sono seni e coseni degli angoli, e poco altro.

Incominciamo dai sistemi di riferimento e dai vettori.

Vettori e sistemi di riferimento

Quello che i vettori sono

I vettori sono astrazioni matematiche, oggetti scaturiti, nel corso del XIX secolo, dalla mente dei matematici, fisici, ingegneri ecc. dopo un lungo periodo di gestazione, una crescita a tratti tormentata ed una definitiva affermazione.

Per chi fosse interessato ad una storia del concetto di vettore, consiglio l’interessante libro di Michael J. Crowe intitolato “A History of Vector Analysis” del 1967

e poi, dello stesso autore, un breve intervento che potrete trovare qui.

Anche la voce corrispondente su Wikipedia merita di essere letta. Purtroppo questi documenti sono tutti in inglese, ma spero che per voi non sia una difficoltà eccessiva.

Quello che i vettori non sono

I vettori non sono delle frecce! Le frecce, che ormai tutti conoscono e usano, sono delle semplici icone, simboli utilizzati per riassumere le proprietà base dei vettori, che però vanno capite e utilizzate correttamente. Per analogia sarebbe un po’ come dire che gli atomi sono dei sistemi solari in miniatura e le molecole sono delle palle collegate da segmenti.

A proposito di icone, ecco un altro libro interessante: “Icons and Symmetries” di Simon L. Altmann, pubblicato nel 1992, da cui ho tratto qualche utile insegnamento.

Adesso basta con i libri e affrontiamo l’argomento “vettore che non è una freccia”.

Sistemi di riferimento

Iniziamo con l’esporre i concetti di base relativi ai sistemi di riferimento e ai vettori e successivamente introduciamo gli operatori di traslazione, rotazione e roto-traslazione di corpi rigidi, limitandoci per semplicità allo spazio tridimensionale.

Lo spazio in tridimensionale cui operiamo, secondo la teoria della relatività generale è uno spazio curvo a causa dell’effetto distorsivo dei corpi dotati di massa.

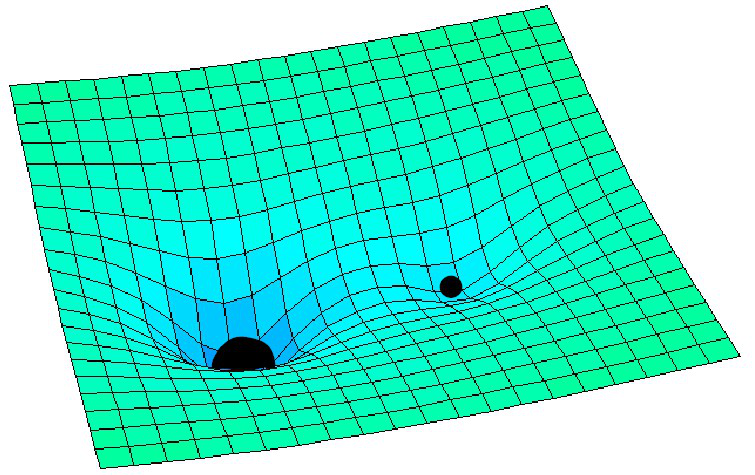
Tuttavia, con ottima approssimazione, possiamo dire che localmente esso può essere considerato non-curvo, cioè piano (occhio, non significa che siamo in un piano, ma che lo spazio non è curvo).

Questo spazio piano prende il nome di spazio Euclideo, perché obbedisce agli assiomi della geometria euclidea (ricordate … due rette parallele non si incontrano mai, ecc. ecc.)

Per caratterizzare i vettori è opportuno, se non necessario, definire all’interno dello spazio euclideo uno o più sistemi di riferimento detti anche terne cartesiane, caratterizzati da un’origine $O$ da cui si irradiano tre segmenti orientati di lunghezza unitaria $\i,\j,\k$, tra loro ortogonali, che poi non sono altro che i soliti assi $x,y,z$.

Indichiamo un sistema di riferimento con uno di questi simboli (io preferisco il primo a sinistra):

Ci sono due modi per posizionare i segmenti orientati, come si può vedere nella figura sottostante

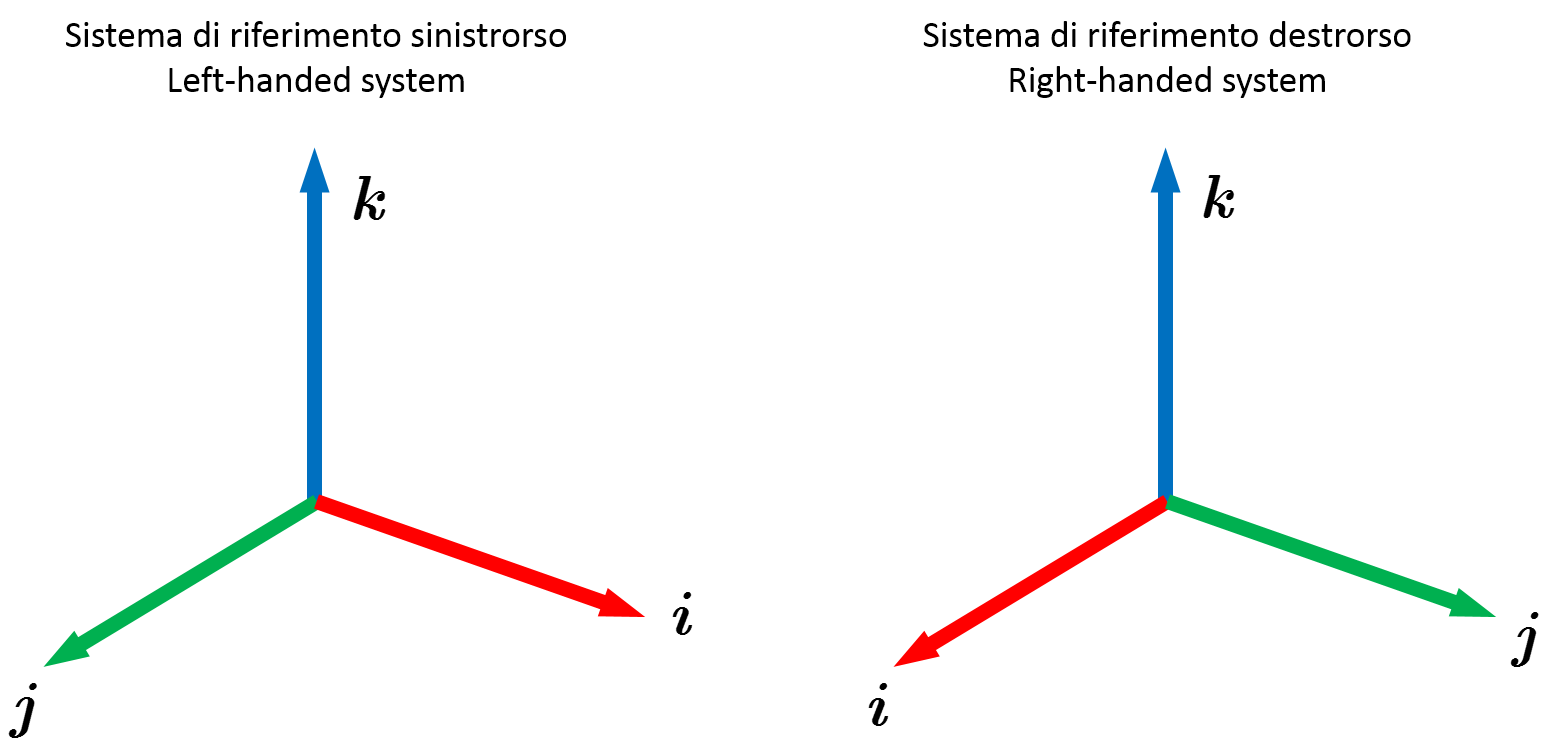
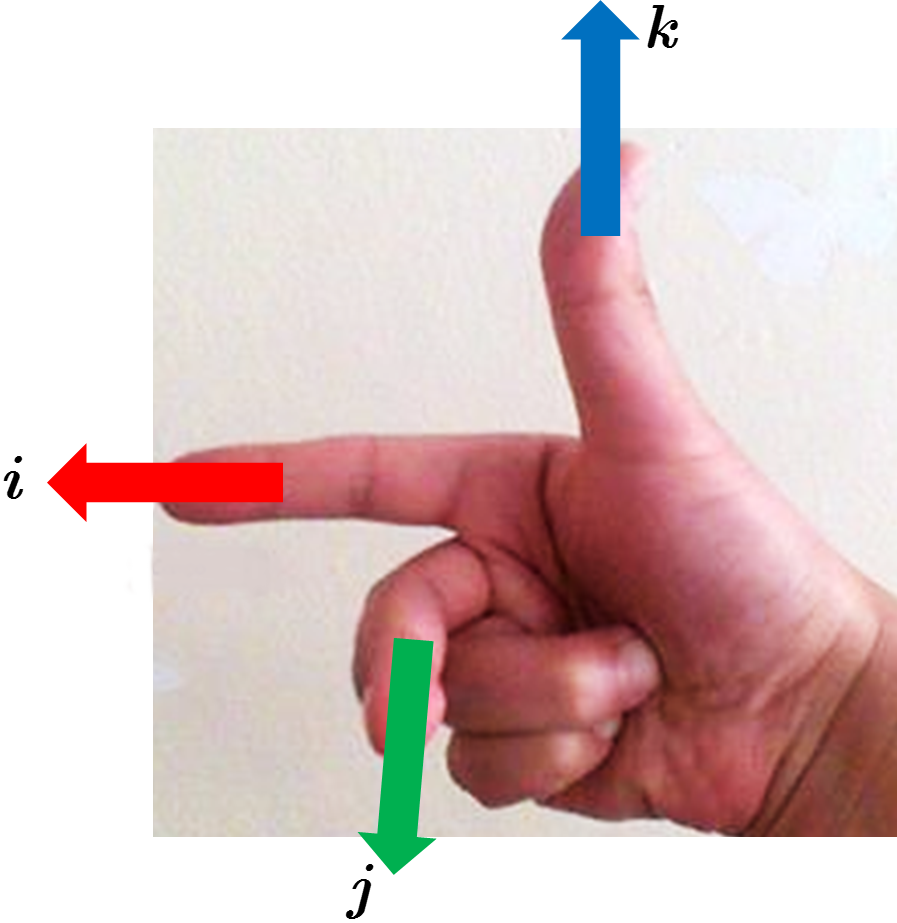
Il modo illustrato sulla sinistra prende il nome di riferimento sinistrorso, mentre quello di destra prende il nome di riferimento destrorso. I nomi derivano da una semplice regola mnemonica: se prendiamo la nostra mano destra e orientiamo $\k$ lungo il pollice, $\i$ lungo l’indice e $\j$ lungo il dito medio, otteniamo un riferimento, appunto, destrorso. Se invece prendiamo la mano sinistra e facciamo la stessa cosa, cioè $k=$ pollice, $\i=$ indice $\j=$ medio otteniamo un sistema di riferimento sinistrorso.

Noi useremo sempre e dovunque il riferimento destrorso, detto anche terna destrorsa.

Vettori

Ci sono due tipi di vettori: i cosiddetti vettori geometrici, che descrivono punti o relazioni puramente geometriche e i cosiddetti vettori fisici, che descrivono grandezze fisiche con certe proprietà.

Vettori geometrici

I vettori geometrici rappresentano le coordinate di un punto geometrico rispetto ad un sistema di riferimento che l’utente ha fissato da qualche parte nello spazio (o nel piano).

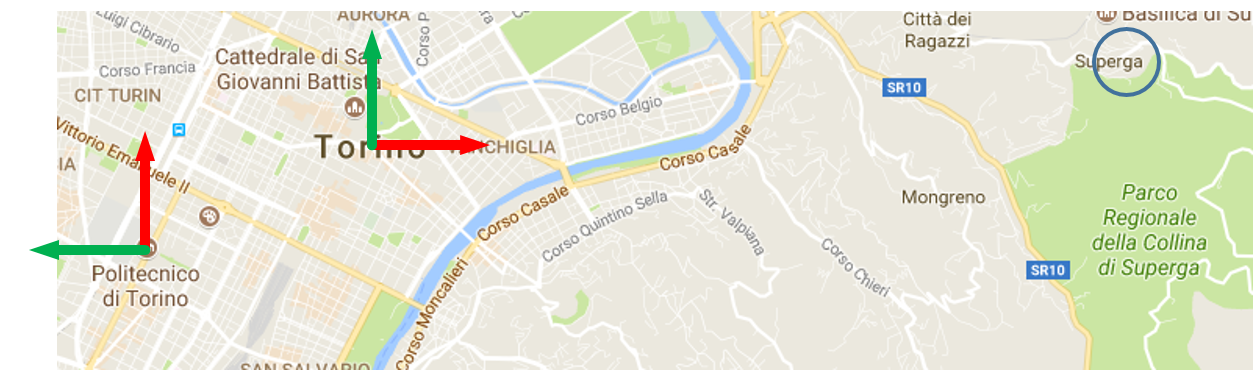
Ad esempio, se fissiamo un sistema di riferimento in Piazza Castello a Torino (O), orientato con $\i$ verso est e $\j$ verso nord, e vogliamo rappresentare il punto geometrico dato dalla basilica di Superga (S), abbiamo il seguente risultato: il segmento $\overrightarrow{OS}$ è lungo approssimativamente 6381 m, e le due componenti sono date in metri dal vettore

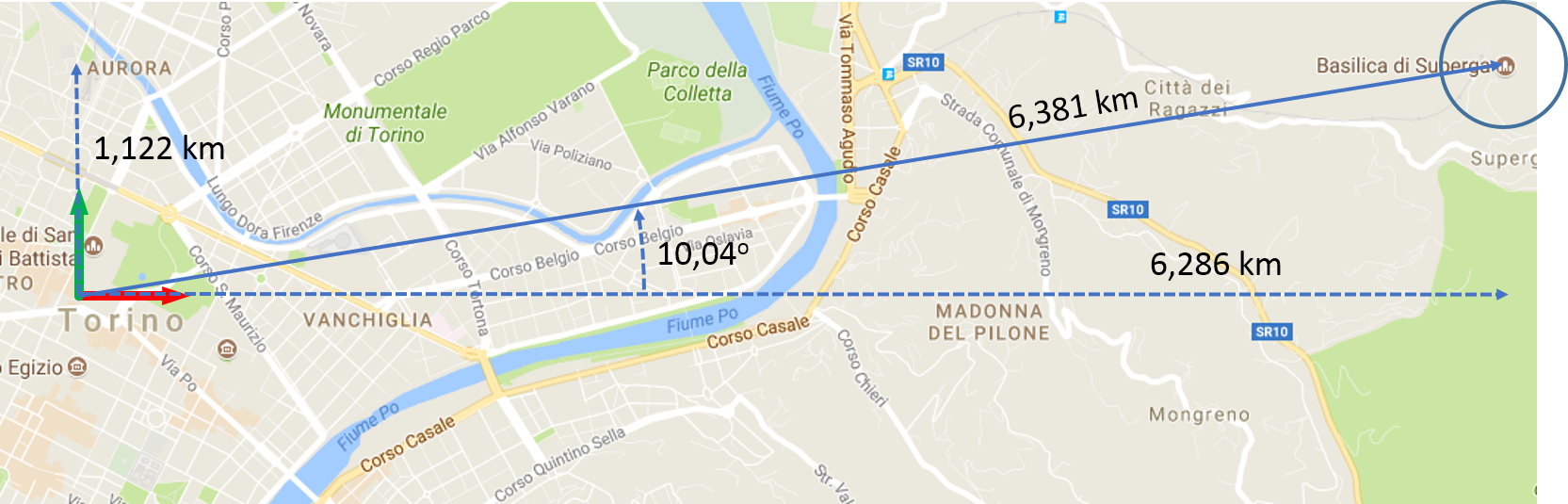
Se spostiamo il sistema di riferimento in un’altra origine, oppure lo ruotiamo, il vettore cambia le sue componenti.

Quindi, prima considerazione, un vettore che rappresenta un punto geometrico non rimane costante al variare della posizione e dell’orientamento del sistema di riferimento.

Adesso vi propongo un quiz: come cambia il vettore $\v$ se poniamo il nostro riferimento al Politecnico, ma con gli assi orientati $\i$ verso nord e $\j$ verso ovest?

Dopo che avrete risposto al quiz, continuerò con un nuovo post, sempre su questi benedetti vettori.

P.S. per fare i calcoli ho usato le coordinate Lat.+Long. datemi da Google Earth e poi le ho convertite in km andando qui. Potevo fare meglio o in modo diverso? Probabilmente sì, e ora aspetto la vostra soluzione …

Back to home