Gradi di Movimento, gradi di libertà

Questo post è dedicato ad illustrare il concetto di ridondanza e di non ridondanza nei robot industriali. Per fare questo è necessario avere chiari alcuni concetti.

Si dice che il braccio umano è ridondante, perché esso è in grado - fortunatamente - di poter, entro certi limiti, far assumere alla mano una posizione nello spazio con diverse configurazioni della catena braccio-avambraccio. Per rendersene conto, basta appoggiare saldamente la mano su una superficie piana, come un tavolo, e, tenendola ferma, muovere il gomito con continuità tra due posizioni che sono più o meno ampie a seconda del grado di “anchilosamento” del soggetto.

Quindi, in maniera per ora qualitativa, possiamo dire che la ridondanza consente di raggiungere una determinata posizione con diverse configurazioni della catena cinematica.

Vediamo ora di essere un po’ meno generici.

In primo luogo occorre ricordare che un robot industriale di solito sposta la sua estremità nello spazio tridimensionale per eseguire vari compiti. L’estremità del robot consiste in una piastra con una serie di fori normalizzati su cui possono essere attaccate le pinze per afferrare gli oggetti, o attrezzi diversi per condurre lavorazioni meccaniche o altro (ad esempio, teste di saldatura a punti o continua, teste di taglio laser, attrezzi per la verniciatura, per la deposizione di collanti o sigillanti, e molte altre).

Di solito questa piastra prende il nome di punta operativa (in inglese Tool Center Point o TCP).

In secondo luogo dovremmo ricordare che un corpo rigido nello spazio è univocamente determinato da sei parametri, tre dei quali individuano la posizione, e altri tre che individuano l’orientamento o assetto.

I primi tre sono di solito specificati utilizzando le coordinate cartesiane $x,y,z$, gli altri tre specificando tre angoli $\phi,\theta,\psi$. Più avanti dedicherò un post a caratterizzare matematicamente l’assetto di un corpo mediante vari tipi di angoli (Eulero, Roll-Pitch-Yaw, e altri) oppure le matrici di rotazione, oppure i quaternioni. Per ora limitiamoci a pensare che siano tre angoli opportunamente definiti.

L’insieme dei sei parametri viene organizzato come un vettore a sei componenti, che prende il nome di posa.

Anticipo brevemente che per me i vettori sono vettori colonna, e se devo metterli in riga, uso il simbolo $^T$ per indicare il vettore trasposto.

La posa è dunque l’informazione di posizione e di assetto di un corpo rigido.

Se poi il corpo si muove solo in un piano, sono sufficienti tre parametri, due di posizione $x,y$ e uno di rotazione $\phi$, che rappresenta l’angolo di rotazione del corpo intorno ad un asse perpendicolare al piano, rispetto ad un valore zero definito dall’utente (di solito l’asse orizzontale). Quindi la posa di un corpo rigido che si muove su un piano è un vettore con tre sole componenti.

Adesso, se vogliamo capire se un robot è ridondante oppure non ridondante, occorre paragonare tra loro due numeri, uno che dipende dal compito che vogliamo effettuare, l’altro che dipende da quanti giunti (gradi di movimento) ha il robot.

Facciamo un esempio sul piano; supponiamo di voler effettuare lo spostamento di un oggetto da una posizione ad un’altra, ma non ci interessa una particolare assetto dell’oggetto, che può essere qualsiasi. Il compito richiede quindi di poter determinare due soli parametri, $x$ e $y$ ad esempio del centro di massa dell’oggetto. Questi li chiamiamo “gradi di libertà” del compito e li indichiamo con $n_c$.

Per essere in grado di svolgere il compito, il nostro robot non potrà avere meno di due giunti, cioè due gradi di movimento che indichiamo con $m$, ma che devono essere opportunamente collocati; infatti, se per disattenzione o ignoranza, collochiamo due giunti prismatici con entrambi gli assi paralleli, ad esempio alla direzione $x$, avremo ottenuto un risultato insoddisfacente perché la punta operativa non potrà che muoversi lungo l’asse $x$ e quindi consentire un solo grado di libertà alla stessa.

Quindi anche se i gradi di libertà del compito e i gradi di movimento del robot sono uguali, bisogna stare attenti a come progettare la catena cinematica, perché dobbiamo fare in modo da garantire che la punta del manipolatore, cioè il TCP, abbia i gradi di libertà richiesti dal compito se non di più (ma comunque non è possibile andare oltre sei). Questi li chiamiamo gradi di libertà della punta operativa e li indichiamo con $n_p$. Se il progettista è saggio e non ci sono ragioni per fare in modo diverso (per esempio, volendo una catena ridondante), vogliamo che sia sempre $m=n_p$.

Nel caso planare considerato il TCP ha due gradi di libertà, il compito richiede due gradi di libertà e quindi abbiamo ottenuto un robot che definiamo non-ridondante, perché $m-n_p=0$.

Pare di capire che la ridondanza si ottiene ponendo più gradi di movimento di quelli necessari a ottenere i gradi di libertà desiderati per la punte operativa, cioè $m\gt n_p$

Si hanno due tipi di ridondanza: la ridondanza intrinseca e la ridondanza estrinseca o relativa al compito.

Ridondanza intrinseca

La prima è quella più comunemente conosciuta come ridondanza senza ulteriori aggettivi. Viene misurata dal grado di ridondanza $m-n_p$. I progettisti la realizzano quando occorre aumentare la cosiddetta manipolabilità che consente al robot di evitare ostacoli che potrebbero rendere impossibili certe lavorazioni, oppure per aumentare lo spazio di lavoro.

Nella figura che segue il robot effettua le lavorazioni su parti che sono sorrette da basi rotanti, in modo da poter eseguire le lavorazioni su ambo i lati del pezzo. In questo caso il sistema di lavorazione possiede 6 + 3 gradi di movimento, ma i gradi di libertà della punta operativa del robot sono sempre pari a 6. Quanti sono i gradi di libertà del pezzo da lavorare? Li sapreste calcolare?

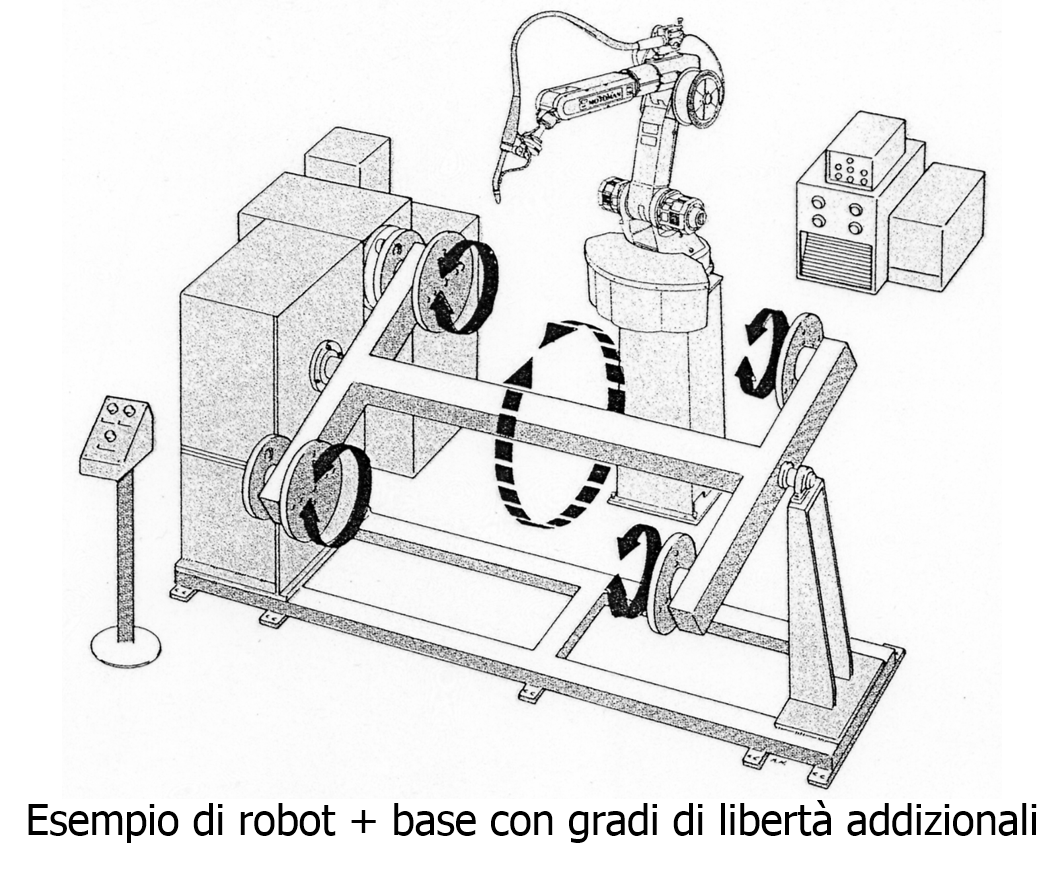
Anche in questo seconda figura si ha una situazione analoga: oltre ai due porta-pezzi rotanti, ora la base del robot trasla su una rotaia, cosa che permette di aumentare il volume dello spazio di lavoro. Il sistema possiede 9 gradi di movimento, ma la punta operativa continua ad avere solo 6 gradi di libertà.

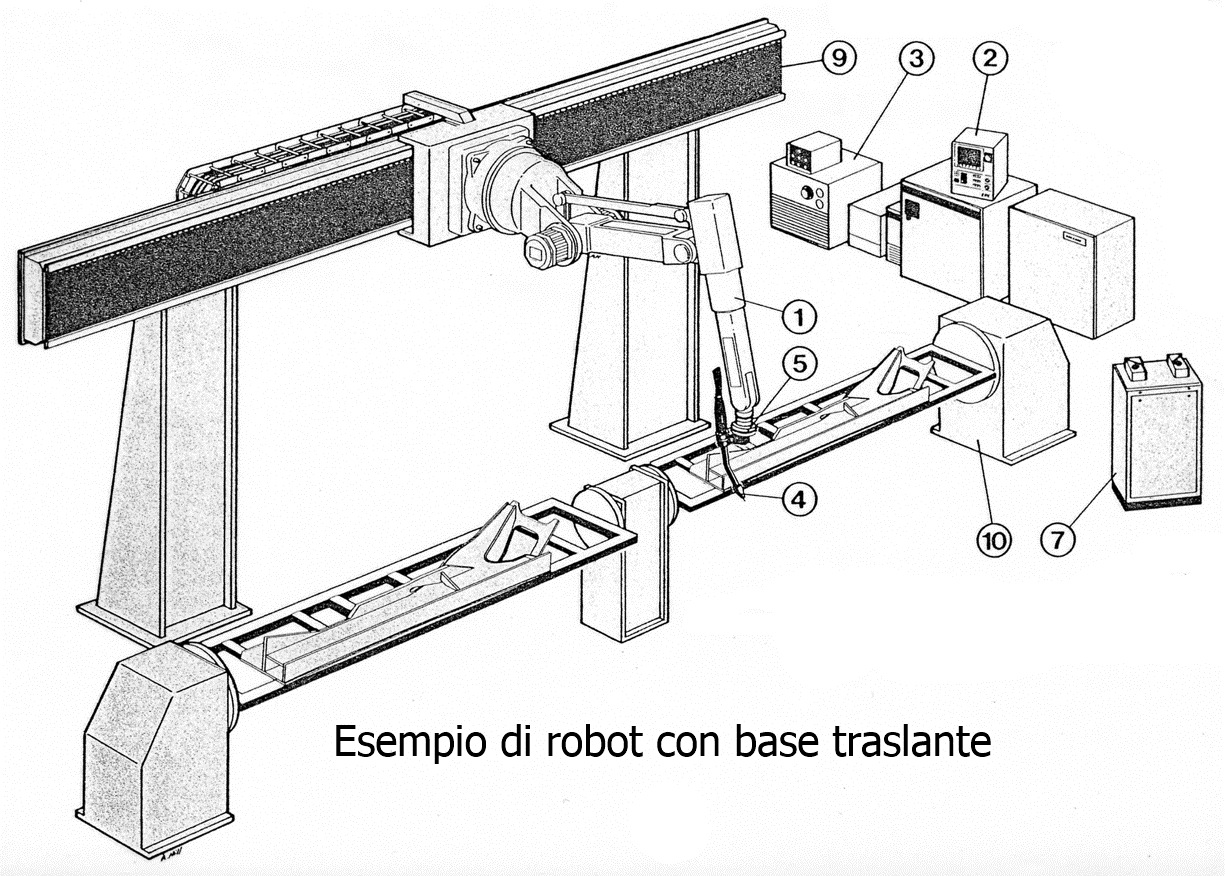
Ridondanza estrinseca

La ridondanza estrinseca, come detto, riguarda il compito. Vediamo alcuni esempi.

1. Supponiamo per semplicità di voler praticare dei tagli su una piastra di metallo con una testa laser attaccata al TCP. Una volta che il laser sia posto alla distanza corretta dal piano di taglio, sono necessari solo due gradi di libertà, perché l’assetto della testa non è importante, essendo l’effetto di taglio sul metallo indipendente dall’orientamento della testa laser.

2. utilizziamo un robot 6R come stampante 3D. Sappiamo che le normali stampanti 3D sono strutture cartesiane a soli 3 gradi di libertà, quindi in questo caso, pur sapendo che il robot 6R non è intrinsecamente ridondante, il compito che deve eseguire lo rende estrinsecamente ridondante.

In conclusione la situazione si può riassumere così: se in un robot i gradi di movimento sono $m$, la punta operativa ha $n_p$ gradi di libertà e se il compito ne richiede $n_c$, allora

• se $m=n_p=n_c$ siamo nella situazione più comune. Il robot non è ridondante, ma perfettamente adatto ad eseguire il compito richiesto. Il numero di giunti è il minimo necessario.

• se $m=n_p\gt n_c$ il robot, pur non essendo intrinsecamente ridondante, lo è nei confronti del compito.

• se $m\ge n_p = n_c$ il robot è intrinsecamente non ridondante.

Negli ultimi anni molte aziende di robot hanno iniziato ad produrre robot con sette gradi di movimento, tutti a giunti rotoidali. Tali robot imitano la struttura del braccio umano, come si vede dalla figura seguente e vengono utilizzati per evitare ostacoli e risolvere problemi di singolarità cinematiche. In un post successivo spiegherò cosa sono queste singolarità

Si veda il video di questo robot ridondante che evita gli ostacoli nello spazio di lavoro.

Bene, il prossimo post sarà dedicato a ripassare il concetto di vettori e matrici, per introdurre poi le matrici di rotazione che sono utlilissime per esprimere l’assetto di un corpo rigido nello spazio e … non solo.

A presto. I commenti sono benvenuti.