La rappresentazione astratta dei bracci robotici - le catene cinematiche

In questo post descrivo le catene cinematiche, che sono una rappresentazione astratta dei bracci robotici. Successivamente sarà possibile discutere le funzioni cinematiche dirette e inverse, cosa che farò in uno dei prossimi post.

Per ragioni di spazio mi limito a considerare la classe dei robot industriali, tralasciando i robot umanoidi o quelli su zampe, anche se i concetti evidenziati qui si possono applicare a queste categorie di robot.

Una catena cinematica rappresenta in sintesi un modello astratto della geometria di un robot fisico e nel fare ciò si introducono alcune ipotesi semplificative.

La prima ipotesi è che ogni parte della catena cinematica sia perfettamente rigida. La rigidezza perfetta non esiste in natura, ma nel nostro caso la diamo per scontata.

La seconda ipotesi è che sul moto delle varie parti della catena cinematica non agiscano forze di attrito di alcun genere.

La terza ipotesi è che il moto della catena cinematica sia generato in modo astratto; cioè per ora non viene introdotto alcun tipo di motore o azionatore. La relazione che le forze/coppie applicate alle masse hanno con la generazione del moto della catena cinematica (e viceversa) sarà descritta in futuro quando parleremo del modello dinamico del manipolatore.

Lo studio delle catene cinematiche fa riferimento quindi alle sole grandezze cinematiche, che sono le posizioni, le velocità e le accelerazioni delle varie parti della catena, prescindendo come detto dall’effetto di forze/coppie interne o applicate dall’esterno.

Detto ciò, una catena cinematica è composta da un certo numero di bracci (in inglese arms o links), ipotizzati privi di massa e, come detto, perfettamente rigidi, collegati tra loro tramite giunti (in inglese joints), anch’essi privi di massa, perfettamente rigidi, su cui non agiscono forze/coppie di attrito.

Il movimento della catena cinematica è reso possibile dalla presenza dei giunti, che permettono un moto relativo tra i bracci ad esso collegati.

I giunti che considero in questa trattazione sono solo di due tipi,

1. di rotazione o rotoidali
2. di traslazione o prismatici

illustrati schematicamente nella figura seguente.

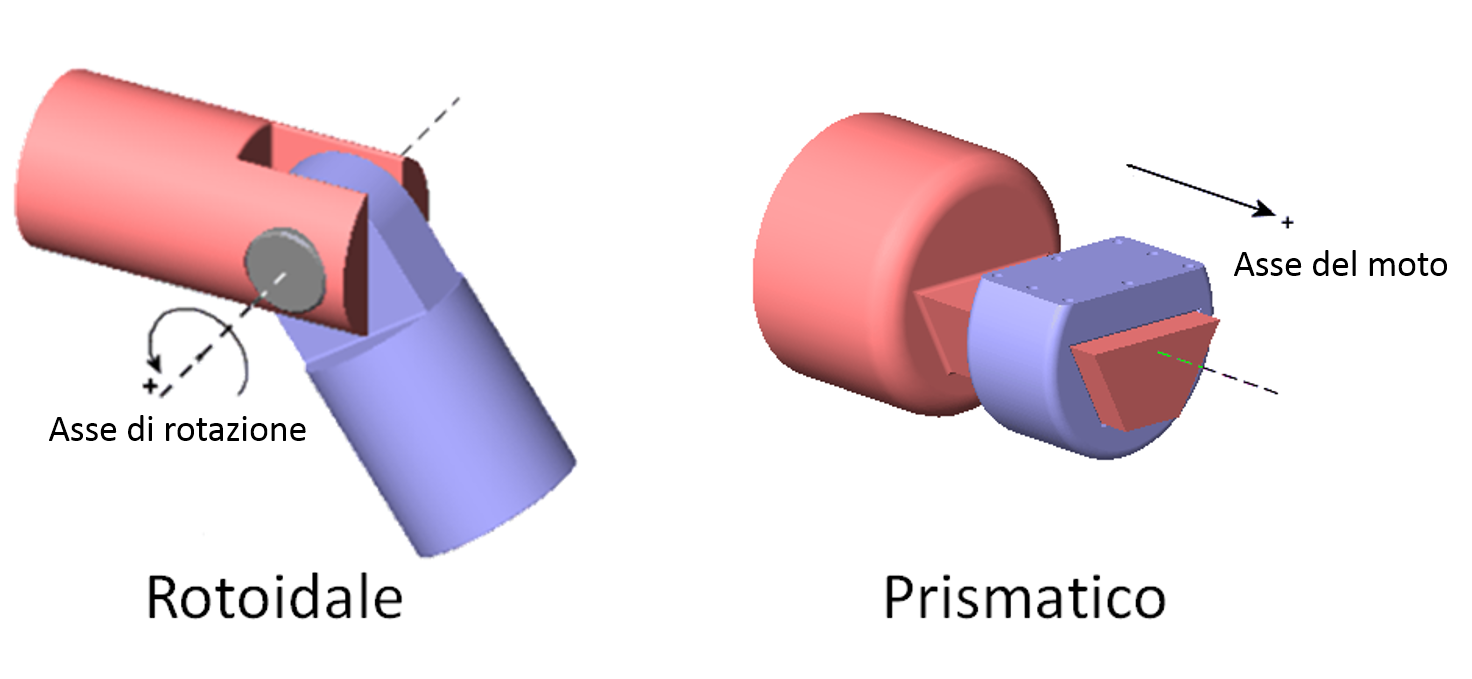
Qui sotto invece è illustrato un tratto di catena cinematica con un braccio e due giunti rotoidali. Come potete osservare, il braccio è rappresentato da un semplice segmento, supposto privo di massa, come pure sono privi di massa i giunti.

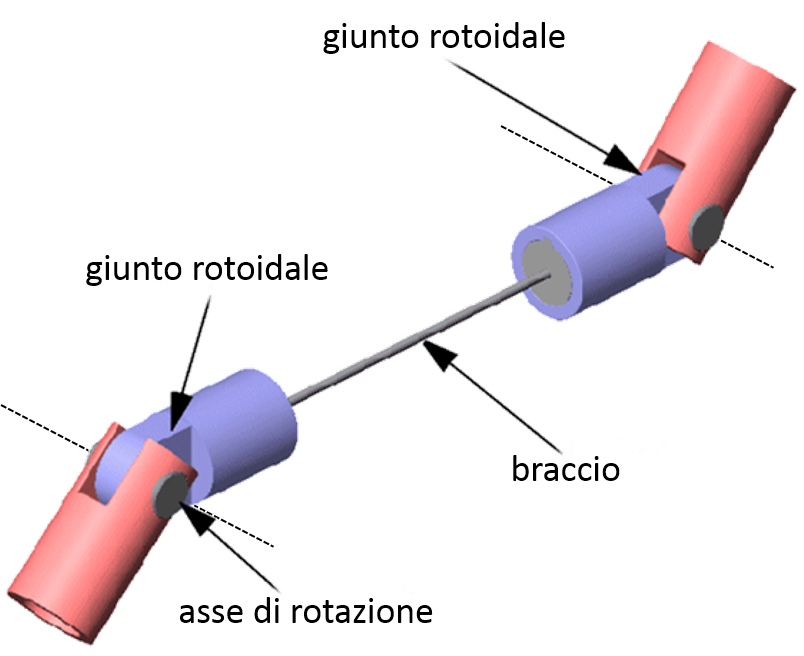
Giunto di rotazione

Il giunto di rotazione permette un movimento di rotazione intorno ad un asse, detto asse di rotazione o asse del moto, che consente di modificare l’angolo tra il braccio a monte del giunto e quello a valle .

Poiché spesso si devono disegnare le catene cinematiche senza aggiungere troppi particolari, si usano rappresentazioni semplificate sia in 3D sia in 2D. Purtroppo la rappresentazione di solito avviene sulla superficie piana di un disegno e quindi bisogna rappresentare la catena in prospettiva.

I giunti di rotazione si rappresentano in 3D come dei cilindri in assonometria ortogonale, orientati secondo la prospettiva desiderata. Nel disegno sottostante si deve immaginare che l’asse $x$ sia orizzontale, l’asse $y$ verticale e l’asse $z$ esca dal piano verso l’osservatore. Le frecce curve indicano il verso positivo del moto angolare, secondo una convenzione che chiariremo in seguito.

Qui sotto invece è illustrata la rappresentazione grafica in 2D, dove i giunti hanno rappresentazioni diverse a seconda del punto di vista (da sopra o di lato) e corrispondono a cerchi oppure a due triangoli affacciati ad un vertice

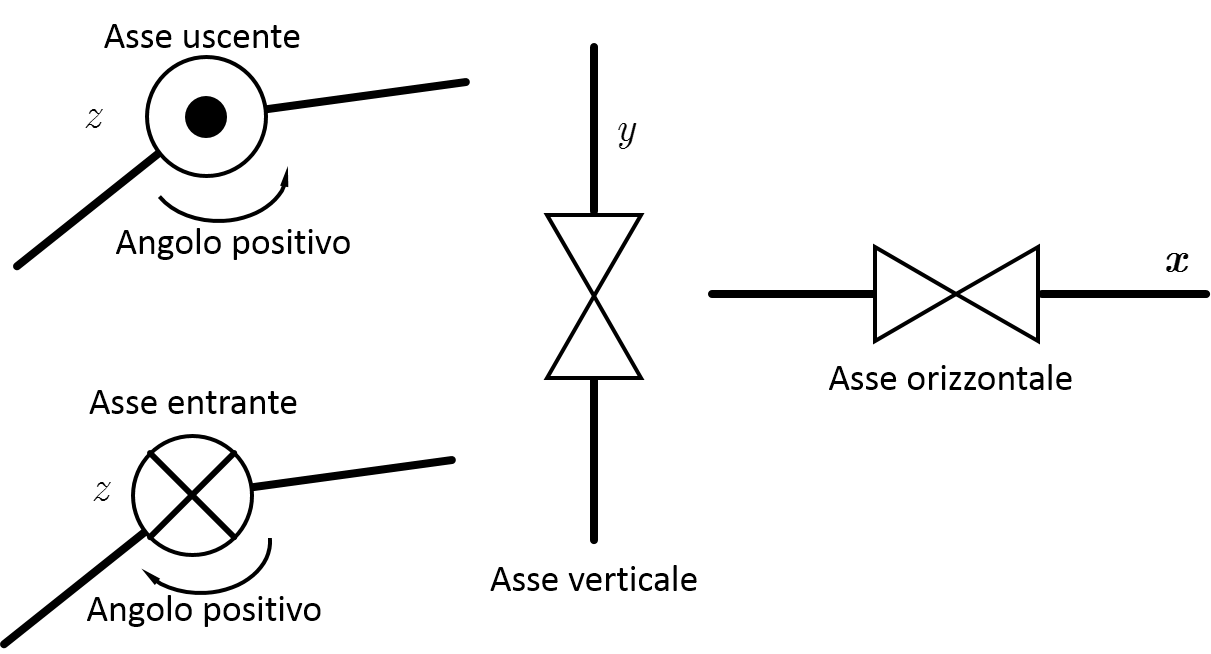
L’asse $z$ nella vista 2D è convenzionalmente quello normale al piano del disegno e può essere indicato con un pallino dentro un cerchio per indicare che “esce” dal piano e il verso positivo dell’angolo è antiorario, mentre si usa una X dentro un cerchio per indicare che “entra” nel piano e il verso positivo è orario. Torneremo più avanti a precisare come determinare il verso di rotazione a seconda del segno dell’angolo, utilizzando la “regola della mano destra” che penso sia nota a tutti voi.

Giunto di traslazione

Il giunto di traslazione, detto anche giunto prismatico, introduce una traslazione lungo un solo asse, detto asse di traslazione o asse del moto, permettendo così ai bracci collegati a monte e a valle di modificare la loro distanza relativa.

I giunti prismatici si rappresentano in 3D con dei cubi o parallelepipedi attraversati da un segmento che rappresenta l’asse di traslazione.

Nella figura a) rappresenta un giunto con asse di traslazione lungo l’asse $z$ normale al foglio, b) un giunto con asse di traslazione lungo l’asse $x$ e assi colineari; c) un giunto con asse di traslazione lungo l’asse $x$, e assi ortogonali; d) un giunto con asse di traslazione lungo l’asse $y$ (assi colineari); e) un giunto con asse di traslazione lungo l’asse $y$ (assi ortogonali).

Esistono anche giunti che permettono una combinazione di traslazioni e rotazioni intorno a più assi come, ad esempio, in un giunto elicoidale, ma nella descrizione delle catene cinematiche non è necessario introdurli.

Gradi di movimento

Esistono anche giunti che permettono una rotazione contemporanea intorno a più assi, come succede, ad esempio, in un joystick, oppure che permettono rotazioni e traslazioni contemporanee, come nel movimento di una vite elicoidale, ma questi non verranno introdotti nella presente descrizione delle catene cinematiche.

I giunti che consideriamo hanno un solo grado di movimento proprio perché permettono o una rotazione intorno ad un singolo asse o una traslazione lungo un singolo asse.

Catene aperte e catene chiuse

Convenzionalmente il basamento su cui si fissa il manipolatore è detto braccio zero (un po’ come la terra nei circuiti elettronici) a cui fa seguito il giunto 1, il braccio 1, il giunto 2, e così via fino al braccio terminale, detto braccio $n$ che ha il compito di portare l’attrezzo o la pinza.

La catena cinematica aperta è quella in cui non ci sono circuiti che si rinchiudono su sé stessi, ossia ogni braccio è collegato ad un solo altro braccio a monte e a valle, salvo il primo, che non ha bracci a monte (tranne il braccio zero) e l’ultimo, che non ha bracci a valle; una catena cinematica chiusa è quella in cui qualche braccio può essere collegato a più di un braccio a monte e/o a valle.

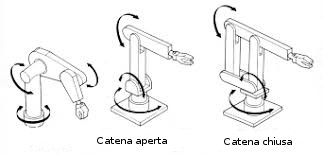
Nella figura che segue sono illustrati i due tipi di catena cinematica

Catena cinematica aperta

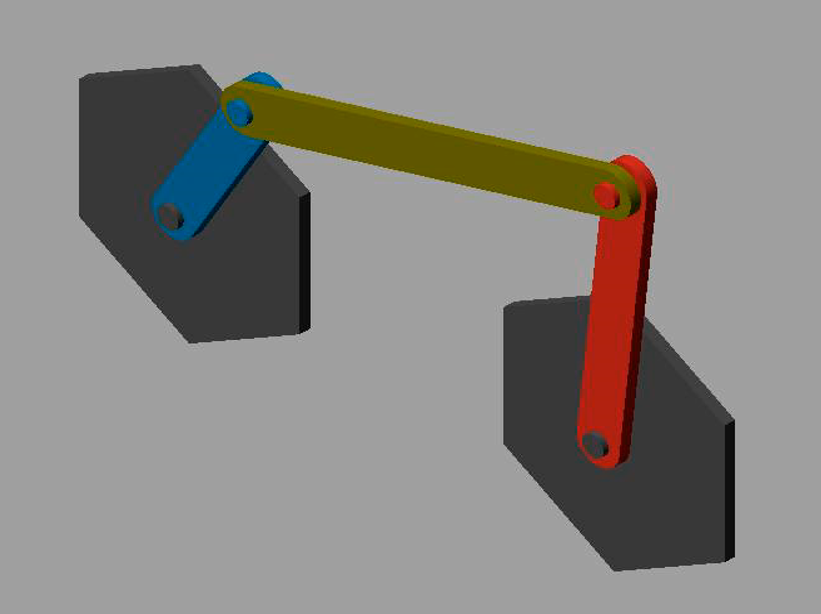Catena cinematica chiusa

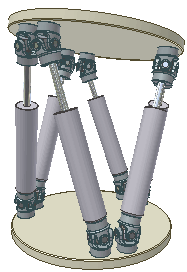
Esistono anche delle catene cinematiche dette a bracci paralleli che sono anche note come piattaforme di Stewart. Sono composte da 6 giunti prismatici collegati a coppie a tre punti di una piasta che sorregge l’attrezzo. Vengono utilizzate per quei movimenti che devono avvenire a grande velocità, ma in un volume di lavoro non troppo grande. Alcune stampanti 3D sono basate su questo tipo di catena cinematica.

Piattaforma di Stewart

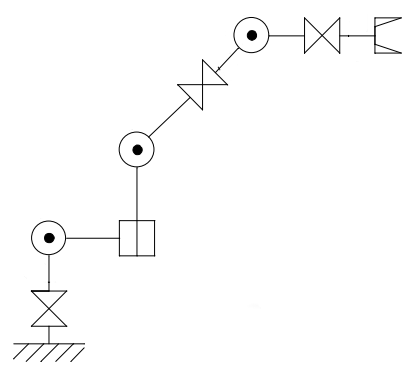
Nelle catene aperte è consuetudine descrivere la catena con una lista di simboli, dove R rappresenta un giunto rotoidale e P un giunto prismatico, a partire dalla base fino alla punta.

Nell’immagine seguente è schematizzata una catena aperta, descritta come R-R-P-R-R-R-R e detta anche 2R-1P-4R, in quanto ci sono 2 giunti di rotazione, quindi 1 giunto prismatico che è seguito da 4 giunti di rotazione. La catena ha perciò 7 gradi di movimento, o meglio. il grado di movimento è 7.

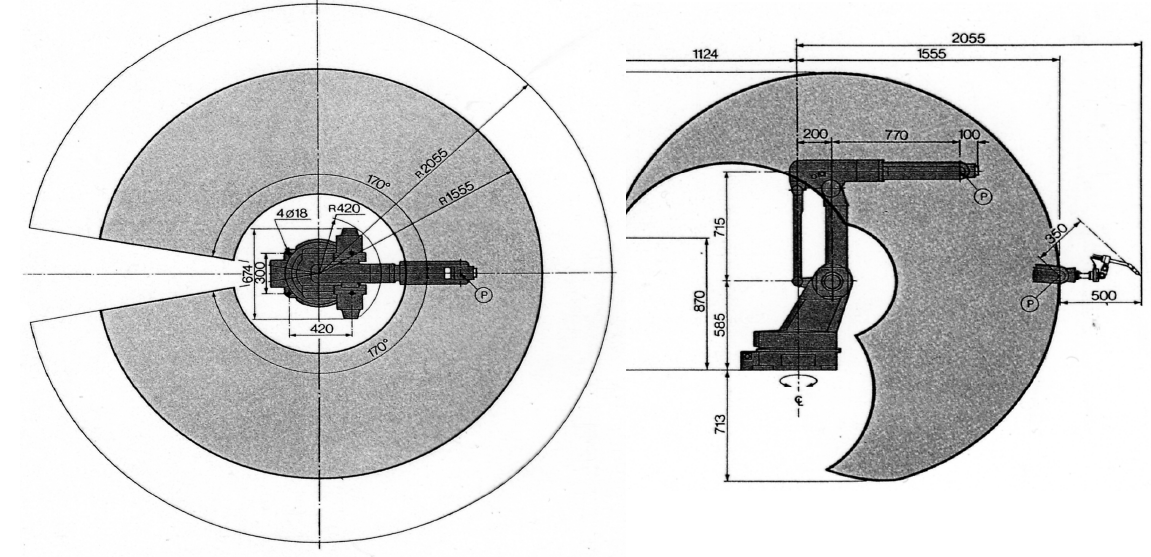
Spazio di lavoro

Si chiama spazio di lavoro del manipolatore il volume di spazio raggiungibile dalla punta operativa, per ogni possibile movimento dei giunti, date la forma e le caratteristiche geometriche dei bracci.

Lo spazio di lavoro è quindi formalmente definibile come un sottoinsieme dello “spazio cartesiano”, cioè lo spazio tridimensionale in cui tutti noi operiamo.

Nello spazio di lavoro vengono definiti un certo numero di sistemi di riferimento cartesiani; ad esempio: il riferimento alla base del robot, il riferimento locale della flangia porta-attrezzo, il riferimento locale del pezzo da manipolare o dell’attrezzo. Tra questi si sceglie il sistema di riferimento principale, ad esempio quello alla base del robot, e si dice allora che i punti in questo riferimento sono dati come coordinate mondo o coordinate assolute; analogamente si definiscono le coordinate attrezzo, le coordinate trasportatore, le coordinate pezzo ecc.

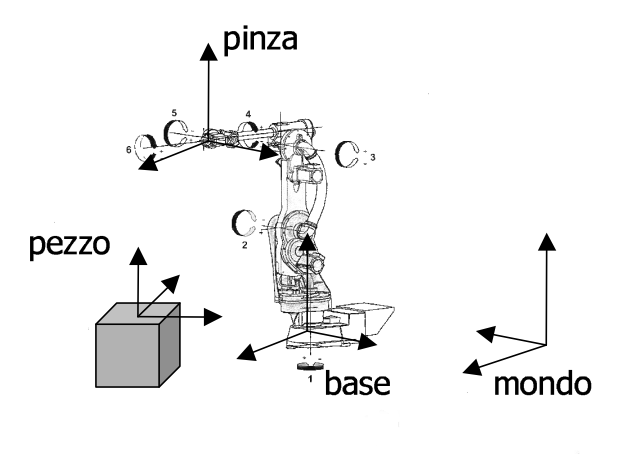
Altri sistemi di riferimento vengono convenzionalmente fissati ai bracci del manipolatore, in un modo che specificheremo in un altro post, per descriverne i movimenti relativi e ottenerne la descrizione cinematica e dinamica. Le rotazioni (ove il giunto è rotoidale) e le traslazioni (ove il giunto è prismatico), definiscono le cosiddette coordinate giunto o coordinate macchina.

Tratterò in dettaglio in uno dei prossimi post i sistemi di riferimento e le rappresentazioni vettoriali di punti geometrici e di variabili fisiche non scalari.

Tipologie di catena cinematica

Sulla base della struttura della catena cinematica è possibile classificare i robot in alcune classi caratteristiche.

I costruttori di robot industriali fanno in modo che i primi tre bracci, che formano quella che viene chiamata spalla, servano a posizionare nello spazio i successivi tre bracci, che costituiscono quello che viene comunemente chiamato polso; a quest’ultimo in genere è affidato il compito di fornire l’orientamento nello spazio della punta operativa.

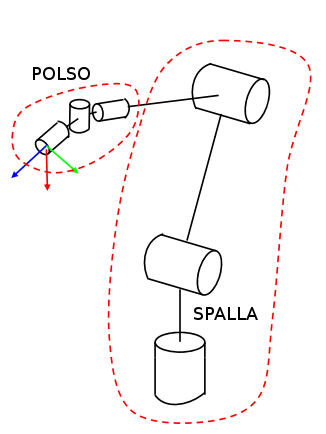
Esistono anche strutture meccaniche a bracci paralleli che non rispettano questo schema spalla-polso; queste strutture vengono chiamate, come abbiamo già visto, manipolatori a cinematiche parallele o, più semplicemente, manipolatori paralleli.

Il polso ha una struttura praticamente standard, di solito R-R-R o 3R, mentre la spalla può essere progettata in molti modi diversi. A seconda della struttura cinematica della spalla, i robot si possono classificare in:

• Robot cartesiani (3P);

• Robot cilindrici (1R-2P);

• Robot polari (2R-1P);

• Robot SCARA (Selective Compliance Assembly Robot Arm) (2R-1P con assi di movimento verticali).

• Robot articolati o antropomorfi (3R);

Robot cartesiano (3P)

La struttura 3P è studiata per fornire tre traslazioni lungo i tre assi ortogonali, da cui il nome di robot cartesiano. Esso può assumere la configurazione a colonna, oppure a “carro-ponte”.

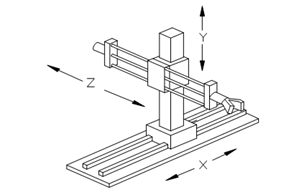
Lo spazio di lavoro di questo tipo di robot è un parallelepipedo.

Robot cilindrico (1R-2P)

Un robot cilindrico realizza le coordinate cilindriche: quindi ad un giunto di rotazione verticale, seguono un primo giunto prismatico, con asse verticale, ed un secondo giunto prismatico, con asse orizzontale. Lo spazio di lavoro corrisponde ad una corona cilindrica.

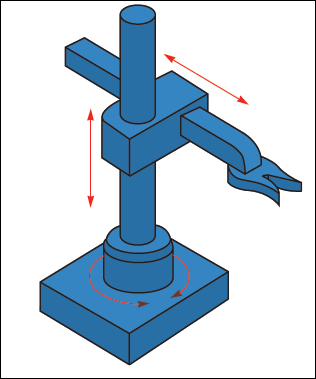
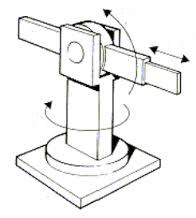
Robot polare (2R-1P)

Il robot polare realizza le coordinate polari: si ha un giunto di rotazione verticale, seguito da un secondo giunto di rotazione, con asse orizzontale, ed un giunto prismatico, con l’asse allineato lungo l’ultimo braccio. Lo spazio di lavoro è una corona sferica.

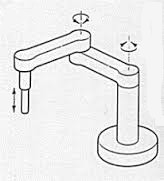
Robot SCARA (2R-1P)

Questo tipo di robot è simile come struttura ad un robot polare, ma si differenzia per il fatto che tutti gli assi dei giunti rotoidali sono verticali; in questo modo l’effetto della gravità è compensato staticamente dalla struttura stessa. Questo tipo di struttura è stato inizialmente concepito per compiti di montaggio di circuiti integrati; la pinza è dotata di un dispositivo più cedevole in alcune direzioni rispetto ad altre (da cui il termine selective compliance), che permette l’inserimento dei pezzi senza causare rotture, come potrebbe avvenire con un dispositivo troppo rigido

Robot articolato o antropomorfo (3R)

Viene comunemente indicato anche con il nome di robot antropomorfo, perché la sua struttura è simile a quella del tronco, braccio e avambraccio umano, su cui si innesta il polso.

Consta di tre giunti rotoidali, il primo dei quali ha solitamente asse di rotazione verticale, mentre gli altri due sono orizzontali.

Il polso

Il polso di un manipolatore ha essenzialmente il compito di fornire i tre gradi di movimento necessari per modificare l’orientamento (o assetto) della punta operativa. Per alcuni manipolatori, con compiti ridotti, il polso è limitato a fornire solo uno o due gradi di movimento.

Le strutture cinematiche più comunemente utilizzate nel polso sono quelle a tre giunti rotoidali, con diversi allineamenti degli assi; si può avere un polso Euleriano, cioè una realizzazione meccanica che realizza gli angoli di Eulero, oppure una realizzazione che viene chiamata Roll-Pitch-Yaw (RPY), che in italiano sono il rollio, il beccheggio e l’imbardata .

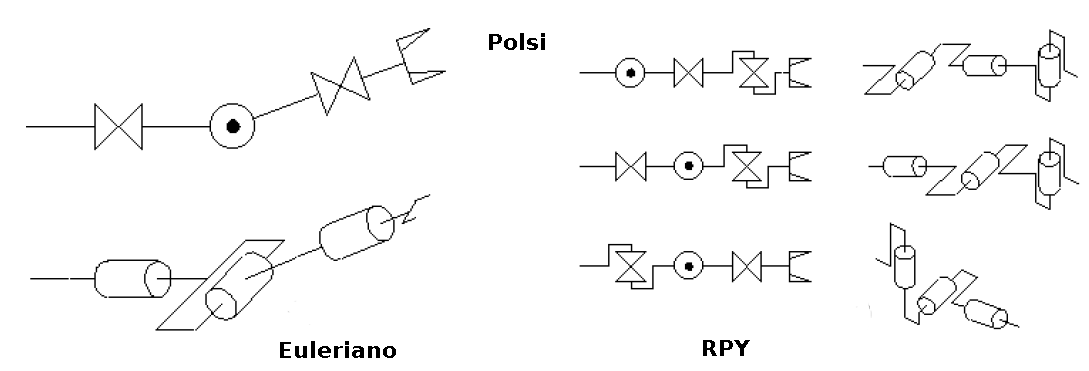
Il polso Euleriano rientra nella categoria dei polsi sferici, ossia quei polsi per cui i tre assi di rotazione si intersecano in un punto. Per un manipolatore robotico avere un polso sferico è molto importante, perché permette una più agevole soluzione della cinematica inversa.

Per concludere questo post, che spero non vi abbia troppo annoiato, i tipici robot industriali hanno questa struttura

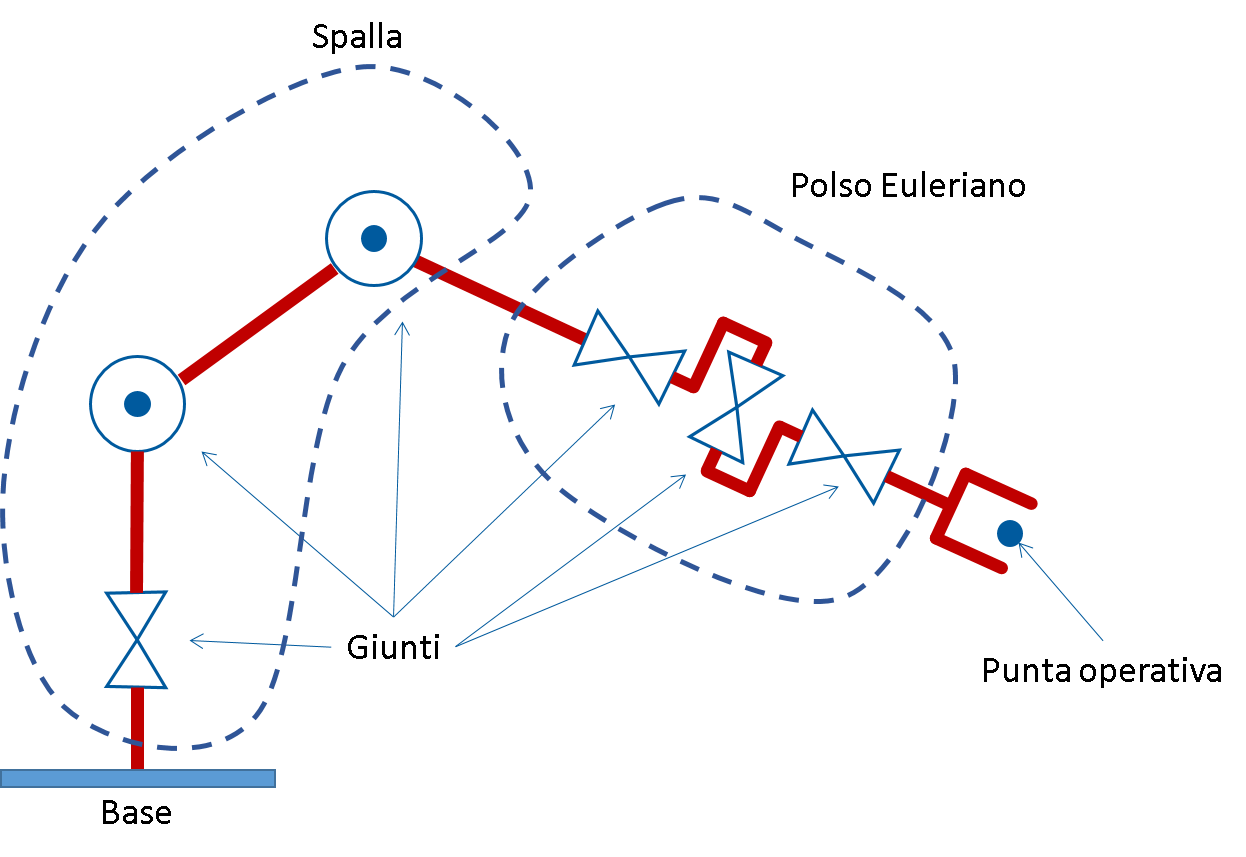
come si vede, ad esempio, nel nuovo robot e.Do della Comau.